Порядок выполнения работы. 1. Выбрать из таблицы 4 в соответствии с вариантом закон распределения интервалов между двумя соседними заявками.

1. Выбрать из таблицы 4 в соответствии с вариантом закон распределения интервалов между двумя соседними заявками.

2. Рассчитать теоретическое значение интенсивности l и вариации v_u.

3. Написать программу, реализующую методику оценки интенсивности потока, описанную в п. 1.3 .

4. При помощи программы произвести оценку интенсивности и коэффициента вариации заданного потока;

5. Построить график зависимости оценок 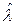и 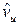от величины N.

4. Варианты заданий

Таблица 4 – Варианты заданий к лабораторной работе №2

5. Содержание отчета

1. Цель работы.

2. Формула и график закона распределения интервалов.

3. Описание разработанной программы: список использованных переменных, список использованных функций, блок-схема, листинг.

4. Графики зависимости оценок интенсивности и коэффициента вариации от M. На графиках уровнем отметить теоретические значения эти величин;

5. Выводы.

6. Вопросы для самопроверки

1. В чем отличие детерминированных потоков от стохастических? Приведите примеры.

2. Приведите характеристики потоков событий.

3. Что такое стационарные и нестационарные стохастические потоки? Приведите примеры.

4. Что такое рекуррентные и нерекуррентные потоки?

5. В чем заключается свойство рекуррентности потока?

6. Как экспериментально вычисляется оценка интенсивности потока?

7. Как экспериментально проверить отсутствие последействия в потоке?

8. Как проверяется гипотеза о нестационарности потока?

7. Список рекомендованной литературы

1. Вентцель Е. С. Теория вероятности. М.: Наука. 1969 г.

2. Строгалев В. П., Толкачева И. О., Имитационное моделирование. М.: Издательство МГТУ им. Баумана, 2008 г.

3. Плакс Б. И. Имитационное моделирование систем массового обслуживания. СПб.: Издательство СПбГААП, 1995.