
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценивание закона распределения случайной величины
Как было отмечено в подразделе 1.1, для качественного моделирования закон распределения вероятностей на выходе датчика случайных чисел должен максимально совпадать с законом распределения для реального процесса. Для оценки закона распределения вероятностей используется экспериментальная гистограмма.
Построение экспериментальной гистограммы сводится к следующим действиям:
1. Определение граничных значений интервала оценивания xmin и xmax.
2. Разбиение интервала (xmin, xmax) на подинтервалы Δ1, Δ2,…, Δn. Количество и длительности подинтервалов выбираются, исходя из требуемой точности.
3. Создание выборки независимых значений случайной величины.
4. Формирование вектора Y=[y1,y2,…,yn]. Компоненты вектора вычисляются по формуле yi= Ni/(N·Δi) где Ni - число элементов выборки, попавших в подинтервал Δi; N – объем выборки.
Гистограммой называется визуальная интерпретация вектора Y. Гистограмма имеет ступенчатый вид. При этом высота «ступеньки» над интервалом Δi равна yi.
Пример 1 .
Дана выборка, объем которой равен десяти: 0, 7, 4, 9, 5, 4, 8, 5, 2, 7. Минимальный элемент выборки равен 0, максимальный – 9. Разобьем интервал [0,9] на три интервала: [0,3), [3,6) и (6,9]. Длины всех трех интервалов одинаковы и равны Δ1=Δ2=Δ3=3. Тогда в первый интервал попадут два элемента (0 и 2), во второй – четыре (4, 4, 5 и 5), в третий – четыре (7, 9, 8, и 7). Вектор Y при этом будет иметь следующий вид:  . Гистограмма данной выборки приведена на рис. 4.
. Гистограмма данной выборки приведена на рис. 4.

Рис. 4. Гистограмма выборки из примера 1.
Теоретическая гистограмма строится следующим образом: высота ступеньки над подинтервалом  равна интегралу от плотности распределения вероятностей по этому подинтервалу.
равна интегралу от плотности распределения вероятностей по этому подинтервалу.
При построении гистограммы важным является правильный выбор объема выборки N, граничных значений xmin и xmax, а также конфигурации подинтервалов. Например, с увеличением N точность результатов моделирования возрастает, но возрастают и затраты на проведение моделирования. Для правильного выбора этих параметров гистограммы разработчику придется решать непростые задачи из области математической статистики, поэтому на практике, как правило, пользуются эмпирическими, инженерными правилами.
Одно из них гласит о том, что если данное событие происходит в процессе моделирования не менее 100 раз, то с вероятностью, близкой к единице, экспериментальная оценка вероятности этого события будет иметь относительную погрешность, меньшую 10%. Это утверждение может быть строго обосновано только для некоторых частных случаев. В то же время, не известны примеры из практики, опровергающие его. Таким образом, для обеспечения приемлемой точности оценивания необходимо увеличивать объем выборки до тех пор, пока не выполнится следующее условие:

Граничные значения анализируемого интервала xmin и xmax должны выбираться так, чтобы вероятность попадания случайной величины за границы данного интервала
Pвне интервала была меньше некой заранее заданной величины. На практике, xmin и xmax, как правило, выбираются таким образом, чтобы Pвне интервала < 0.01.
В задачах, не требующих высокой точности, длительности интервалов Δ1, Δ2,…, Δn выбираются равными ( 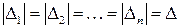 ), а n = 10.
), а n = 10.
С учетом всего вышесказанного обобщенный алгоритм построения гистограммы можно представить следующим образом.
1. Массив выборки A – пустой: xmin = 0, xmax = 0, Ni = 0, N = 0.
2. N = N + 1.
3. Формирование случайного числа x и добавление его к выборке: A=AÈa.
4. Ni = Ni + 1, где i - номер подинтервала, которому принадлежит x.
5.  .
.
6. Если Pвне интервала < 0.01, то левой границей анализируемого интервала назначается минимальный элемент выборки А (xmin = minA), правой границей - максимальный элемент выборки А (xmax = maxA).  . Пересчет всех Ni.
. Пересчет всех Ni.
7. Выполняется условие min{N1,N2,…,Nn} = 100? Если нет, то возврат ко второму шагу.
8. Формирование вектора Y.
9. Построение гистограммы по вектору Y.
2. Цель работы
Изучение алгоритмов получения на ЭВМ чисел с заданным законом распределения и построения гистограмм.
3. Порядок выполнения работы
1. Выбрать из таблицы 3 в соответствии с вариантом закон распределения вероятностей.
2. Вывести соотношение, позволяющее из чисел, сформированных базовым датчиком, получить числа с заданным законом распределения.
3. Написать программу, реализующую датчик случайных чисел с заданным законом распределения. Входными параметрами программы являются характеристики закона распределения и требуемое количество чисел.
4. Написать программу построения гистограммы выборки, сформированной созданным датчиком с учетом параметров, заданных в таблице 2. Программа должна автоматически выбирать конфигурацию подинтервалов и объем выборки. Также должна быть предусмотрена возможность на каждом цикле программы вычислять оценки математического ожидания и дисперсии по текущей выборке.
5. При помощи программы построения гистограмм заполнить таблицу 1. Зафиксировать xmin и xmax.
Таблица 2 – Распределение элементов выборки по квантам гистограммы
| Номер интервала | ||||||||||
| Число элементов, попавших в данный интервал |
6. На основании таблицы 2 построить гистограмму распределения сформированной выборки.
7. Построить график зависимости оценок математического ожидания и дисперсии от объема выборки.
4. Варианты заданий
Таблица 3 – Варианты заданий к лабораторной работе №2
| Номер варианта | Закон распределения | Параметры закона |
| Равномерный | a = 0, b = 5 | |
| Нормальный | m = 0, s = 1 | |
| экспоненциальный | l = 1 | |
| Эрланговский | k = 2, l = 2 | |
| Равномерный | a = -3, b =3 | |
| Нормальный | m = 3, s = 2 | |
| экспоненциальный | l = 2 | |
| Эрланговский | k = 3, l = 4 | |
| Равномерный | a = 10, b = 25 | |
| Нормальный | m = -1, s = 5 | |
| экспоненциальный | l = 3 | |
| Эрланговский | k = 4, l = 2 | |
| Равномерный | a = -15, b = -10 | |
| Нормальный | m = 0, s = 5 | |
| экспоненциальный | l = 4 | |
| Эрланговский | k = 3, l = 1 | |
| Равномерный | a = 2, b = 3 | |
| Нормальный | m = -5, s = 12 | |
| экспоненциальный | l = 5 | |
| Эрланговский | k = 5, l = 3 | |
| Равномерный | a = -10, b = -10 | |
| Нормальный | m = 0.5, s = 0.1 | |
| экспоненциальный | l = 6 | |
| Эрланговский | k = 3, l = 3 | |
| Равномерный | a = 1, b = 6 |
5. Содержание отчета
1. Цель работы.
2. Формула и график моделируемого закона распределения.
3. Описание разработанных программ: список использованных переменных, список использованных функций, блок-схема, листинг.
4. Табличное представление результатов анализа сформированной выборки (данные таблицы 2).
5. Гистограмма сформированной выборки.
6. Графики зависимости оценок математического ожидания и дисперсии от объема выборки. На графиках уровнем отметить теоретические значения эти величин.
7. Выводы.
6. Вопросы для самопроверки
1. Чем отличается плотность распределения вероятности от интегральной функции распределения вероятности? Приведите пример.
2. Как по плотности распределения вероятностей вычислить вероятность попадания случайного значения в заданный интервал?
3. Как по интегральной функции распределения вероятности вычислить вероятность попадания случайного значения в заданный интервал?
4. В чем заключается метод обратного преобразования?
5. Для каких распределений вероятности можно использовать другие методы построения датчиков?
6. Как строится экспериментальная гистограмма?
7. Как выбираются границы области построения гистограммы?
8. Как определить необходимый объем выборки для построения гистограммы?
7. Список рекомендованной литературы
7. Вентцель Е. С. Теория вероятности. М.: Наука. 1969 г.
8. Строгалев В. П., Толкачева И. О., Имитационное моделирование. М.: Издательство МГТУ им. Баумана, 2008 г.
9. Шепета А.П., Орлов А. П., Косенков А. М., Исследование на ЦВМ датчиков случайных чисел. СПб.: СПбГУАП, 1997 г.
10. Бусленко Н. П., Голенко Д. И., Соболь И. М., Срагович В. Г., Шрейдер Ю. А. Метод статистических испытаний (метод Монте-Карло). М.: Физматгиз. 1962 г.
Дата добавления: 2015-02-10; просмотров: 316; Мы поможем в написании вашей работы!; Нарушение авторских прав |