Понятие о производной вектора по скалярному аргументу

При рассмотрении задач кинематики и динамики мы встретимся с необходимостью вычисления производных векторов, имеющих различный физический смысл и являющихся функциями различных скалярных аргументов (времени, дуги и пр.). Поэтому в начале этого параграфа мы определим понятие производной вектора по скалярному аргументу в общем виде, не придавая конкретного физического значения вектору и аргументу.

Пусть вектор задан в какой-либо системе координат как непрерывная функция скалярного аргумента

.

При изменении аргумента будет меняться как модуль вектора , так и его направление. Конец вектора при изменении аргумента описывает кривую – годограф вектора . Пусть – некоторое фиксированное значение аргумента, а – его приращение. Тогда при значении аргумента вектор будет иметь другой модуль и другое направление, чем при значении аргумента, равном .

Разность

называется приращением вектора .

Предел отношения

при , если он существует, называется производной вектора по скалярному аргументу и обозначается через , т.е.

.

Заметим, что вектор всегда направлен по секущей годографа вектора , а значит, и вектор направлен также по секущей. При секущая займет предельное положение, совпадающее с касательной к годографу вектора . Следовательно, производная вектора по скалярному аргументу всегда направлена по касательной к годографу этого вектора.

Приведем без доказательства свойства производной вектора по скалярному аргументу:

1. Производная постоянного по величине и направлению вектора равна

нулю.

2. Производная суммы векторов равна сумме производных, т.е.

.

3. Производные скалярного и векторного произведений векторов

соответственно определяются выражениями:

,

.

Пусть вектор задан в неподвижной прямоугольной системе координат, тогда

,

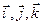где , , – проекции вектора на оси . Так как векторы постоянные, то

.

С другой стороны, вектор можно записать через его проекции следующим образом:

.

Сравнивая оба выражения, найдем проекции производной вектора на координатные оси

, , .

Эти равенства можно прочитать следующим образом: проекции производной вектора на неподвижные оси равны производным от соответствующих проекций вектора.

Модуль производной определяется из равенства

.

Если модуль вектора остается постоянным при изменении аргумента , то годографом вектора будет кривая, расположенная на сфере радиуса . Следовательно, производная , направленная по касательной к годографу вектора , будет в этом случае перпендикулярна вектору .