Криволинейные координаты

Положение точки в трехмерном пространстве, как известно, можно однозначно определить тремя числами. Так, например, в декартовой системе координат такими числами будут координаты 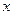, и точки, в цилиндрической и сферической системе координат такими числами будут соответственно , , 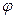и , , 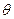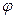. Очевидно, что можно ввести в рассмотрение и другие системы координат, в которых определен закон выбора трех чисел, однозначно определяющих положение любой точки. В этом параграфе мы рассмотрим так называемые криволинейные координаты.

Предположим, что для однозначного определения положения любой точки нами установлен закон выбора трех чисел , тем самым нами введена в рассмотрение определенная система координат. Эти числа называются криволинейными координатами, а введенная система координат – криволинейной. Пусть радиус-вектор, определяющий положение точки , заданной координатами , проведен из произвольно выбранного полюса 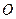. Этот радиус-вектор будет функцией координат :

. (9.38)

Проекции радиуса-вектора на оси декартовой системы координат также будут функциями , т.е.

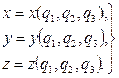(9.39)

Возьмем какую-либо точку с координатами ; тогда уравнения

В которых переменной является только одна координата 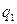, определяет кривую, проходящую через точку . Эту кривую называют координатной линией, соответствующей изменению координаты 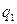. Аналогично определяются координатные линии, соответствующие изменению и .

Касательные к координатным линиям, проведенные в точке в сторону возрастания соответствующих координат, называются координатными осями .

Координатными поверхностями называются поверхности, определяемые уравнениями (9.39) при изменении двух координат и при одной фиксированной координате. Так, например, поверхность определяется следующими уравнениями:

Касательные плоскости, проведенные в точке к координатным поверхностям, называются координатными плоскостями.

Определим теперь единичные векторы координатных осей. Рассмотрим движение точки по координатной линии, соответствующей изменению координаты 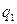. Пусть в момент времени 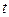точка находится в положении . Вектор , вычисленный в точке , направлен по касательной к координатной линии , т.е. он направлен по координатной оси в сторону .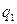

Так как

,

то

. (9.40) Таким образом, единичные вектор равен

. (9.41) Аналогично можно получить

, (9.42)

, (9.43) где

,

. (9.44) Коэффициенты называются коэффициентами Ламе.

Мы будем рассматривать только ортогональные криволинейные координаты, т.е. такие, у которых координатные оси взаимно перпендикулярны. Условием ортогональности является

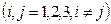. (9.45)

Скорость точки может быть найдена посредством дифференцирования соотношения (9.38)

, (9.46) но так как

, , ,

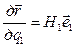то

. (9.47) Учитывая, что по предположению взаимно перпендикулярны, для модуля скорости имеем

. (9.48) Проекции скорости на координатные оси определяются выражениями

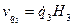, , . (9.49)

Проекция ускорения на координатную ось , очевидно, будет равна

;

отсюда

. (9.50) Взяв частную производную от выражения (9.46) по , получим

. (9.51) Так как производная зависит от координат , то

.

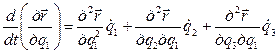Дифференцируя теперь обе части равенства (9.46) по 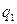, получим

.

Сравнивая оба выражения, найдем

. (9.52)

Подставляя полученные равенства (9.51) и (9.52) в формулу (9.50), имеем

.

Так как , то

.

Аналогично

.

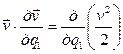Теперь выражение для можно записать в следующей форме:

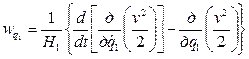, (9.53) где 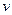находится по формуле (9.48). Аналогично получаем

, (9.54)

. (9.55)

Задачи

Задача 9.12.Найти скорость и ускорение точки в цилиндрической системе координат , , . Координатные линии и координатные оси показаны на рис.

Решение.Так как

, , ,

то, согласно формулам (9.40) и (9.44)

, , .

Следовательно, в соответствии с формулами (9.48) и (9.49), получим

, , (9.56)

и

.

Для полярной системы координат

, , .

Имея в виду, что

,

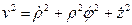найдем

, , ,

, , .

Таким образом, по формулам (9.53), (9.54) и (9.55) получаем

(9.57)

Для полярной системы координат

, .

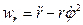Задача 9.13.Найти скорость и ускорение точки в сферической системе координат , , .

Решение.Декартовы координаты связаны со сферическими зависимостями

, , .

Так как

, , ,

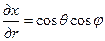то согласно формуле (9.40) имеем

.

Вычисляя далее

, , ,

, ,

и используя формулы (9.44), получим

, .

Следовательно, проекции скорости на координатные оси сферической системы координат равны

, , (9.58)

и

.

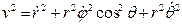Вычислив производные

, , ,

, , ,

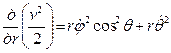найдем проекции ускорения на оси сферических координат:

(9.59)

Задача 9.14.Найти скорость и ускорение точки, движущейся равномерно по винтовой линии.

Решение.Так как в этом случае в цилиндрической системе координат

, ,

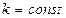( , ), то в силу формул (9.56) имеем

, ,

и, следовательно,

.

Используя формулы (9.57),получим

, , .

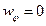Так как , то и . Радиус кривизны .

Задача 9.15.Точка движется по земной поверхности (принимаемой за сферу радиуса 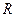), имея северную и восточную составляющие скорости соответственно равными и . Найти ускорение точки относительно Земли, не учитывая ее вращения. Составляющие и считать известными функциями времени.

Решение.Из условия задачи находим

, , .

В соответствии с формулами (9.55) получим

, , .

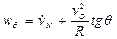Глава X