Нахождение ускорения при координатном способе задания движения.

Пусть движение точки задано в прямоугольной системе координат:

, , .

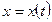Так как вектор скорости точки можно представить в виде

,

то на основании (9.21) будем иметь

.

Пусть 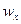, , – проекции ускорения на координатные оси ; тогда

, , , (9.22) т.е. проекция ускорения точки на какую-либо координатную ось равна первой производной по времени от соответствующей проекции скорости точки.

Выражения (9.22) на основании (9.12) можно переписать в виде

, , . (9.23) Следовательно, проекция ускорения точки на какую-либо координатную ось равна второй производной по времени от соответствующей координаты.

Модуль ускорения определяется по формуле

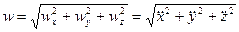. (9.24)

Зная проекции ускорения и его модуль, легко находим направляющие косинусы вектора ускорения:

(9.25)

Найдем теперь ускорение в полярных координатах. Пусть координаты точки заданы как функции времени

, .

Согласно (9.17) имеем

.

На основании (9.21) получим

,

но так как [см. (9.15) и (9.16)]

, ,

то

.

Отсюда находим проекции ускорения на радиальное и поперечное направления

,

. (9.26)

Модуль и направление вектора ускорения определяются по формулам

,

, .