
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Скорость точки
Перейдем теперь к определению понятия скорости точки и методам ее нахождения.
Пусть в момент времени  положение точки определяется радиусом-вектором
положение точки определяется радиусом-вектором  , а в момент
, а в момент  – радиусом-вектором
– радиусом-вектором  . Вектор
. Вектор
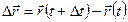
будем называть вектором перемещения за время 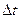 .
.
Отношение вектора  к промежутку времени
к промежутку времени 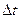 называется средней скоростью точки за промежуток времени
называется средней скоростью точки за промежуток времени 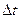
 .
.
 Скоростью в данный момент времени называется предел отношения сектора перемещения точки к промежутку времени, за который произошло это перемещение, когда этот промежуток времени стремится к нулю, т.е.
Скоростью в данный момент времени называется предел отношения сектора перемещения точки к промежутку времени, за который произошло это перемещение, когда этот промежуток времени стремится к нулю, т.е.
 .
.
Размерность скорости будет
 .
.
Единицами измерения могут быть  ,
,  ,
,  .
.
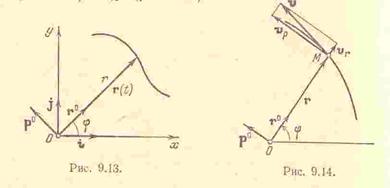
Из этого определения видно, что скорость точки равна произведению радиуса-вектора точки по времени. На рис. показаны средняя скорость  и скорость
и скорость 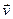 точки
точки  . Как следует из общей теории, скорость точки
. Как следует из общей теории, скорость точки 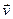 – это вектор, направленный по касательной к траектории в сторону движения точки.
– это вектор, направленный по касательной к траектории в сторону движения точки.
Скорость точки при координатном способе задания движения.Пусть движение точки задано в декартовой системе координат, принятой за неподвижную, т.е. пусть заданы координаты точки как функции времени
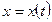 ,
,  ,
,  .
.
Согласно выражению (9.8) имеем
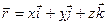 .
.
Так как единичные векторы 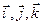 выбранной системы координат постоянны, то на основании формулы (9.11) получаем
выбранной системы координат постоянны, то на основании формулы (9.11) получаем
 .
.
На рис. показано разложение скорости на составляющие по осям координатной системы  .
.
Таким образом, проекции скорости  ,
,  ,
,  на координатные оси будут
на координатные оси будут
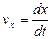 ,
,  ,
,  ,
,
т.е. проекция скорости точки на координатную ось равна первой производной по времени от соответствующей этой оси координаты.
 Так как производную по времени мы условились обозначать точкой сверху, то полученные формулы можно переписать в виде
Так как производную по времени мы условились обозначать точкой сверху, то полученные формулы можно переписать в виде
 ,
,  ,
,  . (9.12)
. (9.12)
Модуль скорости определяется формулой
 , (9.13) а направление скорости – направляющими косинусами
, (9.13) а направление скорости – направляющими косинусами
 (9.14)
(9.14)
Если модуль скорости не изменяется с течением времени, то движение называется равномерным.
Задача 9.4.Движение точки задано уравнениями
 ,
,  ,
,  .
.
Найти скорость точки.
Решение.В соответствии с выражениями (9.12) получим проекции скорости
 ,
,  ,
,  .
.
Модуль скорости определяется формулой (9.13)
 .
.
Направление скорости найдем, используя формулы (9.14)
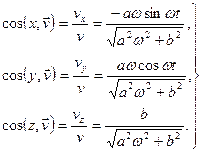
Из этих соотношений видно, что точка движется равномерно  , но направление скорости изменяется с течением времени.
, но направление скорости изменяется с течением времени.
Исследуем траекторию точки. Из первых двух уравнений движения найдем
 .
.
Это – уравнение цилиндра радиуса 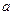 , ось которого совпадает с осью
, ось которого совпадает с осью 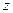 .
.
 Опустим теперь из точки
Опустим теперь из точки  на плоскость
на плоскость 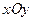 перпендикуляр
перпендикуляр 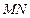 и обозначим угол между осью
и обозначим угол между осью 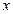 и прямой
и прямой  через
через 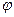 . Координаты точки
. Координаты точки  будут
будут
 ,
,  .
.
Сравнивая эти соотношения с уравнениями движения, найдем
 .
.
Таким образом, угол 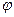 изменяется пропорционально времени. Из этого следует, что прямая
изменяется пропорционально времени. Из этого следует, что прямая  равномерно вращается, а точка
равномерно вращается, а точка  в это время равномерно перемещается по образующей
в это время равномерно перемещается по образующей 
 . Следовательно, точка движется по винтовой линии. Уравнения линии в параметрической форме совпадают с уравнениями движения, а в координатной форме имеют вид
. Следовательно, точка движется по винтовой линии. Уравнения линии в параметрической форме совпадают с уравнениями движения, а в координатной форме имеют вид
 ,
,  .
.
Рассмотрим теперь движение, заданное в полярных координатах, т.е пусть даны как функции времени полярный радиус  и угол
и угол  , определяющие положение точки.
, определяющие положение точки.
Введем в рассмотрение единичные векторы:  , направленный по радиусу-вектору в сторону возрастания
, направленный по радиусу-вектору в сторону возрастания 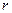 , и
, и  , повернутый относительно
, повернутый относительно  на угол
на угол 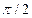 в сторону возрастания угла
в сторону возрастания угла 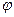 . Единичные векторы
. Единичные векторы  и
и  могут быть представлены через единичные векторы
могут быть представлены через единичные векторы 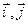 координатных осей:
координатных осей:
 ,
,
 .
.
В дальнейшем нам будут нужны выражения для производных по времени от единичных векторов  ,
,  .
.
Дифференцируя  по времени, получим
по времени, получим
 . (9.15) Аналогично
. (9.15) Аналогично
 . (9.16)
. (9.16)
Радиус вектор  , определяющий положение точки, может быть представлен в виде
, определяющий положение точки, может быть представлен в виде 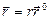 . При движении точки меняются как модуль, так и направление радиуса-вектора
. При движении точки меняются как модуль, так и направление радиуса-вектора  , следовательно, и
, следовательно, и  , и
, и  являются функциями времени. На основании равенства (9.11) имеем
являются функциями времени. На основании равенства (9.11) имеем
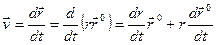 .
.
Используя соотношение (9.15), будем иметь
 .
.
Полученная формула дает разложение вектора скорости на две взаимно перпендикулярные составляющие: радиальную  и поперечную
и поперечную  .
.
Проекция скорости на радиальное и поперечное направления
 и
и 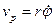 (9.17) называются соответственно радиальной и поперечной скоростями.
(9.17) называются соответственно радиальной и поперечной скоростями.
Модуль скорости находится по формуле
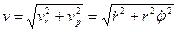 . (9.18)
. (9.18)
Формулу (9.18) можно получить, используя связь между декартовыми и полярными координатами,
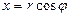 ,
,  .
.
Продифференцировав эти соотношения по времени  ,
,  и используя равенство (9.13), получим
и используя равенство (9.13), получим
 .
.
Нахождение скорости при естественном способе задания движения.Пусть точка  движется по какой-либо кривой. За промежуток времени
движется по какой-либо кривой. За промежуток времени 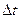 точка переместится из положения
точка переместится из положения  в положение
в положение  . Дуга
. Дуга  , если движение точки происходит в сторону положительного отсчета дуги, и
, если движение точки происходит в сторону положительного отсчета дуги, и  если, если движение происходит в противоположную сторону. На основании (9.11) имеем
если, если движение происходит в противоположную сторону. На основании (9.11) имеем
 .
.
Перепишем это равенство в виде
 .
.
 Так как предел отношения дуги к стягивающей ее хорде равен по модулю единице, а предельное положение секущей
Так как предел отношения дуги к стягивающей ее хорде равен по модулю единице, а предельное положение секущей  совпадает с направлением касательной к кривой в точке
совпадает с направлением касательной к кривой в точке  ,то
,то
 ,
,
где  – единичный вектор касательной к кривой, направленный в сторону положительного отсчета дуги.
– единичный вектор касательной к кривой, направленный в сторону положительного отсчета дуги.
Действительно, если  , то вектор
, то вектор  направлен в сторону
направлен в сторону  , а при
, а при  вектор
вектор  направлен в сторону, противоположную
направлен в сторону, противоположную  . В обоих случаях этот вектор, а следовательно, и его предел
. В обоих случаях этот вектор, а следовательно, и его предел  , направлены в сторону возрастания дуги
, направлены в сторону возрастания дуги  (на рис. положительное направление отсчета дуги
(на рис. положительное направление отсчета дуги  выбрано вправо от начала отсчета
выбрано вправо от начала отсчета  ).
).
Принимая во внимание, что
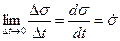 ,
,
имеем
 . (9.19)
. (9.19)
Обозначая  , получим
, получим
 . (9.20) Из формулы (9.20) следует, что
. (9.20) Из формулы (9.20) следует, что  . Очевидно, что
. Очевидно, что  , если движение происходит в сторону положительного отсчета дуги, и
, если движение происходит в сторону положительного отсчета дуги, и  , если движение происходит в противоположную сторону.
, если движение происходит в противоположную сторону.
Так как проходимый точкой путь всегда положителен, то элемент пути
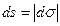
и, следовательно, модуль скорости можно определить по формуле
 .
.
Задачи
Задача 9.5.Если ось 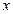 направить горизонтально, а ось
направить горизонтально, а ось 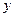 вертикально вверх, то движение тяжелой точки (например, артиллерийского снаряда) у поверхности Земли в предположении, что сопротивление воздуха пропорционально скорости точки, будет описываться уравнениями
вертикально вверх, то движение тяжелой точки (например, артиллерийского снаряда) у поверхности Земли в предположении, что сопротивление воздуха пропорционально скорости точки, будет описываться уравнениями
 ,
,
 ,
,
где  ,
,  ,
,  ,
,  – постоянные величины.
– постоянные величины.
Найти модуль и направление скорости в начальный момент времени. Найти наибольшую высоту  подъема точки над уровнем ее начального положения, дальность
подъема точки над уровнем ее начального положения, дальность  по горизонтали от начального положения точки до ее наивысшего положения.
по горизонтали от начального положения точки до ее наивысшего положения.
Решение.На основании (9.12) имеем
 ,
,
 .
.
При 
 ,
,  , а модуль
, а модуль 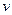 скорости будет
скорости будет
 .
.
Направление скорости определим, найдя направляющие косинусы при  :
:
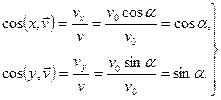
Следовательно, начальная скорость, равная по модулю  , направлена под углом
, направлена под углом  к горизонту.
к горизонту.
Так как точка траектории, где  , соответствует наибольшей высоте подъема движущейся точки, то из уравнения
, соответствует наибольшей высоте подъема движущейся точки, то из уравнения
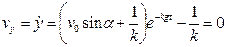
мы определим момент времени  достижения точкой наивысшей высоты. Имеем
достижения точкой наивысшей высоты. Имеем
 ;
;
отсюда
 .
.
Подставляя найденное значение  в выражение для
в выражение для 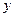 , получим искомую высоту
, получим искомую высоту
 .
.
Найдем теперь расстояние по горизонтали от начального положения точки до ее положения в наивысшей точке. Для этого подставим время  в выражение для
в выражение для 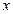 :
:
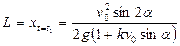 .
.
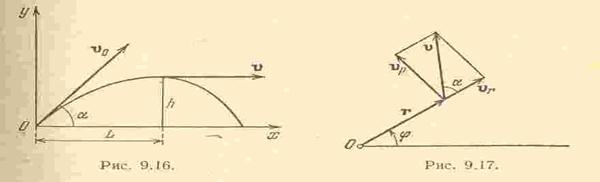 Задача 9.6.Точка движется так, что ее радиус-вектор образует со скоростью постоянный угол. Определить уравнение траектории в полярных координатах, если угол, образуемый скоростью с радиусом-вектором, равен
Задача 9.6.Точка движется так, что ее радиус-вектор образует со скоростью постоянный угол. Определить уравнение траектории в полярных координатах, если угол, образуемый скоростью с радиусом-вектором, равен  .
.
Решение.Согласно формуле (9.17) проекции скорости на радиальное и поперечное направления будут
 ,
, 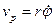 .
.
По условию задачи
 .
.
Следовательно,
 .
.
Отсюда
 .
.
Интегрируя это уравнение и приняв при  угол
угол  , получим
, получим
 .
.
Тогда  , где
, где  – модуль радиуса-вектора
– модуль радиуса-вектора  в момент времени
в момент времени  . Таким образом, траектория представляет собой логарифмическую спираль.
. Таким образом, траектория представляет собой логарифмическую спираль.
Если угол  , то траектория будет прямолинейной – движение будет происходить вдоль радиуса-вектора. Если угол
, то траектория будет прямолинейной – движение будет происходить вдоль радиуса-вектора. Если угол 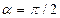 , то движение будет происходить по окружности, так как
, то движение будет происходить по окружности, так как  .
.
Дата добавления: 2015-04-15; просмотров: 419; Мы поможем в написании вашей работы!; Нарушение авторских прав |