
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Частные случаи движения точки
Прямолинейное движение.Если траектория точки является прямой линией, то, направляя одну из координатных осей, например, ось 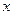 вдоль этой прямой, мы полностью определим положение точки заданием ее абсциссы как функции времени, т.е.
вдоль этой прямой, мы полностью определим положение точки заданием ее абсциссы как функции времени, т.е. 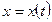 .
.
Проекции скорости и ускорения на ось 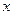 согласно формулам (9.12) и (9.23) будут
согласно формулам (9.12) и (9.23) будут
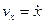 ,
, 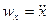 .
.
Модули скорости и ускорения соответственно равны
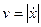 ,
, 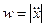 .
.
Если 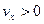 , то движение точки происходит в сторону положительного направления оси
, то движение точки происходит в сторону положительного направления оси 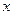 . Если при этом
. Если при этом  , то движение ускоренное, если же
, то движение ускоренное, если же  , то движение замедленное.
, то движение замедленное.
При 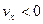 точка движется в направлении, противоположном положительному направлению оси
точка движется в направлении, противоположном положительному направлению оси 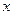 . Если при этом
. Если при этом  , то движение замедленное, если же
, то движение замедленное, если же  , то движение ускоренное.
, то движение ускоренное.
В качестве примера рассмотрим прямолинейное движение, происходящее по закону
 ,
,
где 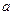 ,
, 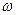 ,
, 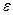 – постоянные величины.
– постоянные величины.
Движение точки по такому называют гармоническим.
Величина 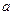 , равная максимальному отклонению точки от положения
, равная максимальному отклонению точки от положения 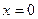 , называется амплитудой колебаний;
, называется амплитудой колебаний;  называется фазой и
называется фазой и 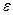 – начальной фазой колебаний.
– начальной фазой колебаний.
Скорость и ускорение точки, совершающей гармоническое колебание, соответственно будут
 ,
, 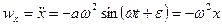 .
.
Из формулы для 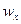 следует, что ускорение точки всегда будет направлено к началу координат и по модулю пропорционально отклонению точки от начала координат.
следует, что ускорение точки всегда будет направлено к началу координат и по модулю пропорционально отклонению точки от начала координат.
С помощью закона движения и формулы для скорости нетрудно установить, что если для какого-либо момента времени  координата
координата 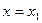 , а скорость
, а скорость  , то в момент времени
, то в момент времени  , при котором
, при котором
 ,
,
где  скорость точки и ее положение будут такими же, как и в момент
скорость точки и ее положение будут такими же, как и в момент  .
.
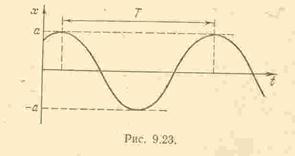
Значит, гармоническое движение будет периодическим, т.е. через промежутки времени, равные
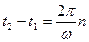 ,
,
движение будет полностью повторяться.
Наименьший промежуток времени, по истечении которого движение повторяется, называется периодом колебаний. Очевидно, что период гармонических колебаний будет равен
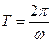 .
.
Число колебаний в единицу времени называется частотой колебаний и равно 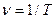 . Если время измеряется в секундах, то частота измеряется в герцах. Величина
. Если время измеряется в секундах, то частота измеряется в герцах. Величина 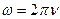 называется круговой частотой. Круговая частота равна числу колебаний за
называется круговой частотой. Круговая частота равна числу колебаний за  единиц времени.
единиц времени.
Движение точки по окружности.При движении точки по окружности удобно задать ее движение в полярных координатах, так как при этом координата  является постоянной величиной, равной радиусу
является постоянной величиной, равной радиусу 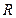 окружности. Положение точки вполне определяется углом
окружности. Положение точки вполне определяется углом 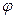 .
.
Так как 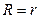 – величина постоянная, то проекция скорости на радиальное направление
– величина постоянная, то проекция скорости на радиальное направление 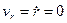 . Поперечная проекция скорости равна
. Поперечная проекция скорости равна
 .
.
Модуль скорости будет
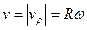 ,
,
где  .
.
В соответствии с формулами (9.26) проекции ускорения на радиальное и поперечное направления определяются равенствами
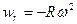 ,
, 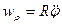 .
.
Модуль ускорения равен

 ,
,
где 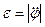 .
.
Если выбрать направление положительного отсчета дуги, проходимой точкой, как указано на рисунке, то очевидно, что касательное ускорение точки будет равно  , а нормальное
, а нормальное 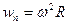 (это ускорение называют центростремительным ускорением).
(это ускорение называют центростремительным ускорением).
Заметим, что 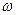 определяет угловую скорость вращения радиуса
определяет угловую скорость вращения радиуса  , а
, а 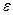 – соответствующее угловое ускорение.
– соответствующее угловое ускорение.
Задачи
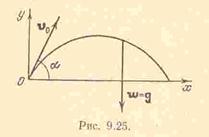
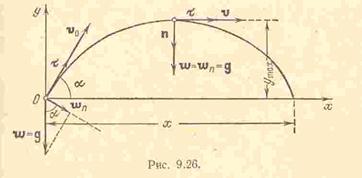
Задача 9.7.Снаряд движется в вертикальной плоскости согласно уравнениям 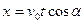 ,
, 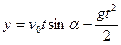 . Определить скорость и ускорение снаряда в начальный момент времени, высоту траектории, дальность полета, а также радиус кривизны в начальной и наивысшей точках траектории. Ось
. Определить скорость и ускорение снаряда в начальный момент времени, высоту траектории, дальность полета, а также радиус кривизны в начальной и наивысшей точках траектории. Ось 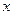 направлена горизонтально, а ось
направлена горизонтально, а ось 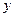 – вертикально вверх.
– вертикально вверх.
Решение.Траекторией снаряда, очевидно будет парабола
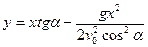 .
.
Определим сначала скорость движения снаряда. Имеем
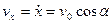
 .
.
Следовательно,
 .
.
В момент времени  величина скорости
величина скорости 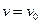 . Направление скорости определяется по формулам
. Направление скорости определяется по формулам
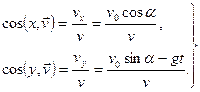
При  получим
получим
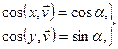
т.е. скорость в начальный момент образует с осью 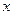 угол
угол 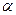 .
.
Проекции ускорения на координатные оси будут
 ,
, 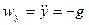 ,
,
следовательно, модуль ускорения равен
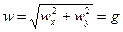 ,
,
и оно направлено по вертикали вниз (ускорение свободного падения). Под высотой траектории понимается максимальное значение ординаты 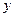 . Очевидно, что
. Очевидно, что 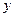 принимает максимальное значение при
принимает максимальное значение при  , т.е. когда
, т.е. когда
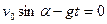 .
.
Находя отсюда 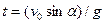 и подставляя его в уравнение для
и подставляя его в уравнение для 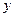 , получим
, получим
 .
.
Дальность полета определяется из условия 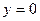 . Из уравнения
. Из уравнения
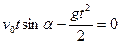
найдем
 ,
,  .
.
Момент  соответствует начальному положению снаряда. Подставляя
соответствует начальному положению снаряда. Подставляя 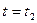 в уравнение для
в уравнение для 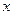 , найдем дальность полета
, найдем дальность полета
 .
.
Максимальная дальность полета будет при  и равна
и равна
 .
.
Найдем теперь радиус кривизны траектории в начальной и наивысшей ее точках. Из формулы  имеем
имеем
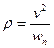 .
.
Таким образом, задача нахождения радиуса кривизны траектории сводится к нахождению скорости и проекции ускорения на нормаль.
Согласно (9.33) имеем
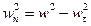 .
.
Так как движение точки происходит все время в сторону возрастания дуги,  , и, следовательно,
, и, следовательно,
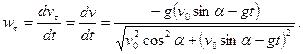
При 
 , а так как
, а так как  , то
, то 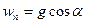 и, следовательно, радиус кривизны траектории в начальной точке равен
и, следовательно, радиус кривизны траектории в начальной точке равен
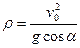 .
.
Для момента времени  , соответствующего наивысшей точке траектории,
, соответствующего наивысшей точке траектории,  , поэтому
, поэтому 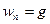 .
.
Скорость точки в этот момент равна 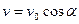 и радиус кривизны в наивысшей точке траектории будет
и радиус кривизны в наивысшей точке траектории будет
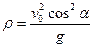 .
.
Отметим, что в данной задаче проекцию ускорения на нормаль в начальной и наивысшей точках траектории можно легко найти и простым проектированием.
 Задача 9.8.Колесо радиуса
Задача 9.8.Колесо радиуса 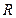 катится без скольжения по горизонтальному рельсу. Скорость центра колеса постоянна и равна
катится без скольжения по горизонтальному рельсу. Скорость центра колеса постоянна и равна 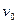 . Найти уравнения движения точки
. Найти уравнения движения точки 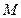 , лежащей на ободе колеса, ее траекторию, скорость, ускорение и радиус кривизны траектории как функцию времени.
, лежащей на ободе колеса, ее траекторию, скорость, ускорение и радиус кривизны траектории как функцию времени.
Решение.По условию, колесо катится без скольжения, следовательно, дуга 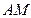 равна отрезку
равна отрезку 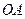 при предположении, что в начальный момент времени точка
при предположении, что в начальный момент времени точка 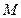 находилась в точке
находилась в точке 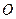 .
.
Так как дуга 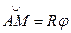 , а
, а 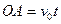 , то
, то  и
и 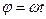 , где
, где 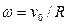 .
.
Координаты точки  будут:
будут:
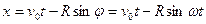 ,
,
 .
.
Эти уравнения можно рассматривать как параметрические уравнения траектории, которая представляет собой циклоиду.
Проекции скорости точки на оси 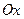 и
и 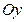 равны
равны
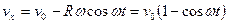 ,
,
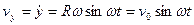 .
.
Модуль скорости равен
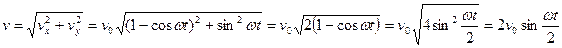 .
.
Заметим, что угол 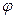 изменяется от нуля до
изменяется от нуля до  и поэтому
и поэтому  .
.
Направляющие косинусы вектора скорости будут
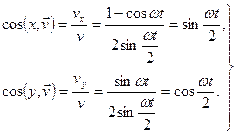
Отсюда следует, что вектор скорости все время проходит через верхнюю точку колеса.
Проекции ускорения на оси 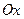 и
и 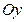 равны
равны
 ,
,
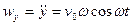
и, следовательно,
 ,
,
а так как
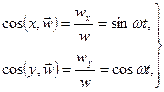
то вектор ускорения точки 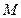 всегда проходит через центр колеса.
всегда проходит через центр колеса.
Радиус кривизны траектории найдем из выражения
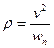 .
.
Так как  и при
и при 
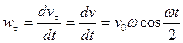 , то
, то
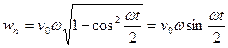 .
.
Следовательно,
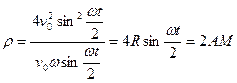 ,
,
где 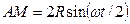 – длина отрезка от рассматриваемой точки колеса до его нижней точки.
– длина отрезка от рассматриваемой точки колеса до его нижней точки.
 Задача 9.9.Движение точки
Задача 9.9.Движение точки 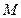 задано в полярных координатах уравнениями
задано в полярных координатах уравнениями 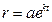 и
и 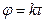 , где
, где 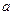 и
и  – постоянные величины.
– постоянные величины.
Найти уравнение траектории, скорость, ускорение и радиус кривизны траектории точки как функции ее радиуса  .
.
Решение. Исключая из уравнений 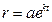 и
и 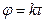 время
время  , получим уравнение траектории
, получим уравнение траектории
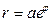 .
.
Это – уравнение логарифмической спирали.
Согласно формуле (9.17) радиальная и поперечная составляющие скорости соответственно будут
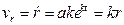 ,
,
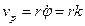 .
.
Следовательно, скорость точки 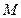 равна
равна
 .
.
Согласно формулам (9.26) будем иметь
 ,
,
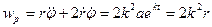 ,
,
т.е. ускорение точки 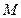
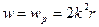 .
.
Определим теперь радиус кривизны траектории. На основании (9.32) получим
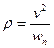 .
.
Скорость 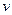 нами уже определена. Найдем
нами уже определена. Найдем 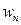 . Согласно (9.33)
. Согласно (9.33)
 ;
;
имеем
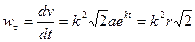 .
.
Таким образом,
 .
.
Итак, радиус кривизны траектории
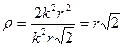 .
.
Задача 9.10.Радар 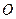 , установленный на берегу, непрерывно следит за движением судна
, установленный на берегу, непрерывно следит за движением судна 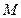 , определяя в каждый момент расстояние
, определяя в каждый момент расстояние  и угол
и угол  между меридианом и направлением радара на судно, а также скорости изменения этих величин. Пренебрегая кривизной земной поверхности, определить модуль скорости судна
между меридианом и направлением радара на судно, а также скорости изменения этих величин. Пренебрегая кривизной земной поверхности, определить модуль скорости судна 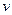 относительно Земли, его курс (угол
относительно Земли, его курс (угол 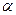 между меридианом и скоростью
между меридианом и скоростью 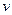 ) и расстояние
) и расстояние  от радара до направления скорости
от радара до направления скорости 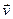 .
.
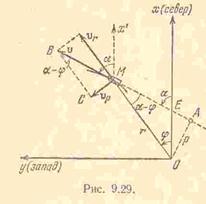
Для решения задачи построим прямоугольную систему координат  , направив ось
, направив ось 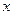 по касательной к меридиану на север, а ось
по касательной к меридиану на север, а ось 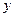 по касательной к параллели на запад. Величины
по касательной к параллели на запад. Величины  ,
, 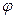 ,
,  и
и 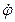 , которые непрерывно измеряет радар, суть полярные координаты судна и их скорости. Поэтому модуль скорости будет (9.18):
, которые непрерывно измеряет радар, суть полярные координаты судна и их скорости. Поэтому модуль скорости будет (9.18):
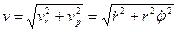 .
.
Для определения курса (угла 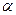 ) разложим вектор скорости судна
) разложим вектор скорости судна 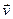 на радиальную
на радиальную 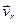 и поперечную
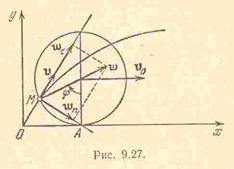
и поперечную 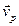 составляющие. Имеем (см. рис.):
составляющие. Имеем (см. рис.):
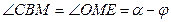
(углы  и
и 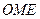 – соответственные при параллельных прямых
– соответственные при параллельных прямых 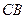 и
и 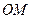 , а
, а  – внешний для треугольника
– внешний для треугольника 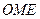 ).
).
Из треугольника 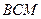 найдем
найдем
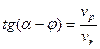 ,
,
или, учитывая значения проекций поперечной 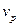 и радиальной
и радиальной 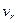 составляющих скорости
составляющих скорости 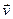 ,
,
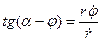 . (9.34)
. (9.34)
Отсюда
 . (9.35)
. (9.35)
Из треугольника 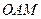 найдем параметр
найдем параметр  :
:
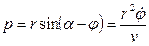 . (9.36)
. (9.36)
С помощью компьютера скорость судна 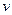 , его курс
, его курс 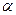 и параметр
и параметр  непрерывно определяются по формулам (9.18), (9.35) и (9.36) или им эквивалентным.
непрерывно определяются по формулам (9.18), (9.35) и (9.36) или им эквивалентным.
Если судно идет постоянным курсом 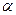 , т.е. движется по прямой линии
, т.е. движется по прямой линии  , то равенство (9.36) определяет уравнение траектории судна в полярных координатах. Покажем, что при
, то равенство (9.36) определяет уравнение траектории судна в полярных координатах. Покажем, что при  это уравнение может быть получено из равенства (9.34).
это уравнение может быть получено из равенства (9.34).
 Действительно, умножая числитель и знаменатель
Действительно, умножая числитель и знаменатель
правой части равенства (9.34) на 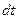 , получим
, получим
 ,
,
или
 .
.
Интегрируя обе части этого равенства и учитывая, что по предположению  , получим
, получим
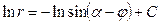 , (9.37) где
, (9.37) где  – произвольная постоянная интегрирования. При
– произвольная постоянная интегрирования. При 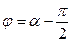 расстояние от радара до судна будет равно
расстояние от радара до судна будет равно  , т.е.
, т.е. 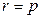 . Подставляя эти значения в (9.37), найдем
. Подставляя эти значения в (9.37), найдем
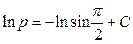
или
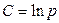 .
.
Внося это значение для  в равенство (9.37), получаем
в равенство (9.37), получаем
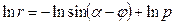 ,
,
откуда следует равенство (9.36)
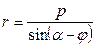 .
.
Задача 9.11.Угол 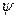 между неподвижной осью
между неподвижной осью 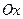 и кривошипом
и кривошипом 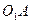 изменяется по закону
изменяется по закону 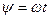 , где
, где 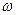 – постоянное положительное число. С кривошипом в точке
– постоянное положительное число. С кривошипом в точке  шарнирно соединен стержень
шарнирно соединен стержень 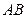 , проходящий постоянно через качающуюся муфту
, проходящий постоянно через качающуюся муфту 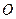 . Найти уравнения движения точки
. Найти уравнения движения точки 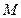 стержня
стержня 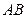 , отстоящей от точки
, отстоящей от точки  на расстоянии
на расстоянии 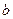 , ее траекторию, скорость и ускорение, если
, ее траекторию, скорость и ускорение, если  .
.
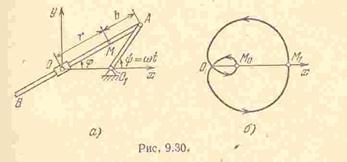
Решение. Положение точки 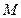 проще всего определяется полярными координатами: радиусом
проще всего определяется полярными координатами: радиусом  и полярным углом
и полярным углом 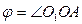 . Так как треугольник
. Так как треугольник 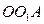 равнобедренный, то
равнобедренный, то 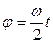 , а сторона
, а сторона 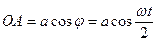 . Из рис. имеем
. Из рис. имеем 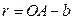 ; следовательно, уравнения движения точки
; следовательно, уравнения движения точки 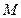 будут:
будут:
 ,
,
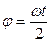 .
.
Исключая отсюда время 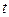 , найдем уравнение движения точки
, найдем уравнение движения точки 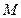 в полярных координатах:
в полярных координатах:
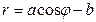 .
.
(Для сравнения самостоятельно найти уравнения движения и траекторию в декартовых координатах).
На рис. показана траектория точки 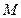 , построенная по точкам для случая
, построенная по точкам для случая 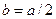 (при
(при  получается обычная кардиоида). Точка
получается обычная кардиоида). Точка 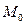 – начальная точка траектории, соответствующая моменту времени
– начальная точка траектории, соответствующая моменту времени 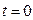 или
или 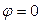
 . Направление движения точки
. Направление движения точки 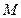 показано стрелками. Отметим, что точка
показано стрелками. Отметим, что точка 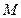 попадет в свое начальное положение
попадет в свое начальное положение 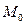 не через один оборот кривошипа
не через один оборот кривошипа 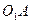 , а через два оборота, когда угол
, а через два оборота, когда угол 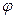 изменится на
изменится на 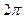 , а угол
, а угол 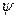 на
на 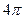 радиана (это произойдет в момент времени
радиана (это произойдет в момент времени  ).
).
Найдем проекции скорости точки на радиальное и поперечное направления. Имеем
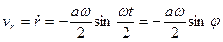 ,
,
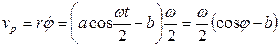 .
.
Теперь найдем модуль скорости точки 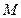 :
:
 ,
,
или, подставляя найденные значения для 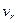 и
и 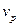 и произведя очевидные преобразования, получим
и произведя очевидные преобразования, получим
 .
.
Для ускорения будем иметь:
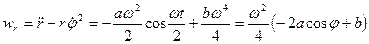 ,
,
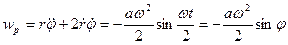 .
.
Модуль ускорения
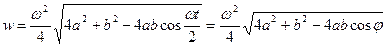 .
.
В начальной точке 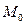 при
при 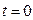
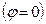 :
:
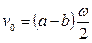 ,
,
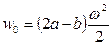 .
.
Через один оборот кривошипа 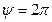 ,
, 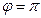 точка
точка 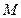 попадет в положение
попадет в положение 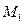 и ее скорость и ускорение будут соответственно равны
и ее скорость и ускорение будут соответственно равны
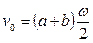 ,
,
 .
.
Дата добавления: 2015-04-15; просмотров: 582; Мы поможем в написании вашей работы!; Нарушение авторских прав |