
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ускорение точки. Предположим, что в момент времени скорость точки равна , а в момент времени
 Предположим, что в момент времени
Предположим, что в момент времени  скорость точки равна
скорость точки равна 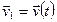 , а в момент времени
, а в момент времени  будет
будет 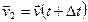 . Изменение вектора скорости за промежуток времени
. Изменение вектора скорости за промежуток времени 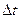 найдем как разность векторов
найдем как разность векторов  и
и  , если параллельно перенесем вектор
, если параллельно перенесем вектор  в точку
в точку  .
.
Вектор  представляет собой приращение вектора скорости за промежуток времени
представляет собой приращение вектора скорости за промежуток времени 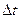 .
.
Отношение вектора  к промежутку
к промежутку 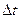 называется средним ускорением точки за промежуток времени
называется средним ускорением точки за промежуток времени 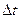 :
:
 .
.
Ускорением  точки в данный момент времени называется предел приращения скорости
точки в данный момент времени называется предел приращения скорости  к приращению времени
к приращению времени 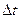 при условии, что последнее стремится к нулю, т.е.
при условии, что последнее стремится к нулю, т.е.
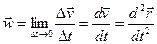 , (9.21) так как
, (9.21) так как  . Можно также воспользоваться следующей формой записи
. Можно также воспользоваться следующей формой записи  .
.
Следовательно, ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной по времени от радиуса-вектора точки.
 Годографом скорости называется кривая, которую вычерчивает конец вектора скорости при движении точки, если вектор скорости проводится из одной и той же точки.
Годографом скорости называется кривая, которую вычерчивает конец вектора скорости при движении точки, если вектор скорости проводится из одной и той же точки.
Очевидно, что скорость точки, вычерчивающей годограф скорости равна  , т.е. ускорению точки при ее движении по траектории. Размерность ускорения
, т.е. ускорению точки при ее движении по траектории. Размерность ускорения
 .
.
Единицами ускорения могут быть  ,
,  .
.
Дата добавления: 2015-04-15; просмотров: 281; Мы поможем в написании вашей работы!; Нарушение авторских прав |