Движение твердого тела называется плоским, если все точки тела перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.

Примером плоского движения тела может служить качение цилиндра по горизонтальной плоскости, при котором его основание остается все время парпаллельным плоскости .

Рассмотрим произвольное плоское движение твердого тела. Пусть все точки тела перемещаются в плоскостях, параллельных плоскости 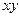. Из определения плоского движения и из свойств твердого тела (углы между любыми прямыми, фиксированными в твердом теле, сохраняются неизменными) следует, что любая прямая , проведенная в теле перпендикулярно плоскости 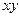, будет перемещаться поступательно, т.е. траектории, скорости и ускорения всех точек этой прямой будут одинаковы.

Таким образом, для определения движения тела необходимо знать движениен лишь одной точки на каждой прямой, проведенной перпендикулярно плоскости .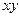

Взяв точки в одной плоскости, параллельной плоскости 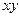, мы можем утверждать, что плоское движение твердого тела вполне определяется движением плоской фигуры, полученной от пересечения тела любой плоскостью , параллельной плоскости .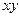

Таким образом, задание движения твердого тела сводится к заданию движения одного его сечения. Поэтому вдальнейшем будем изображать только плоскую фигуру – сечение тела и изучать движение точек этого сечения в его плоскости.

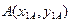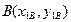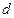Пусть и – две точки плоской фигуры, находящейся в плоскости . Так как расстояние между этими точками остается неизменным

, то из четырех координат независмыми остаются только три. Присоелинение третьей точки не увеличивает числа независимых координат, ибо две новые координаты 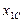и должны удовлетворять двум равенствам, выражающим неизменность расстояний до ранее выбранных точек 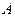и . Таким образом, для описания плоского движения тела требуется знать три независимых координаты как функции времени.

Свяжем жестко с плоской фигурой систему координат . Тогда положение системы , а вместе с ней и положение плоской фигуры относительно системы координат будет вполне определено заданием координат и точки 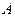и углом между осями и б – см. рис. 11.3, б (оси и 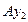соответственно параллельны осям 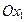и 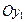и перемещаются при движении фигуры поступательно). Следовательно, три функции времени

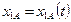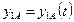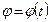, , (11.1) определяют положение плоской фигуры в любой момент времени. Равенства (11.1) называются уравнениями движения плоской фигуры или уравнениями плоского движения твердого тела.