Геометрическое место мгновенных центров скоростей, отмеченных на плоскости, жестко связанных с фигурой, называется подвижной центроидой.

При качении цилиндра по горизонтальной плоскости (рис.11.12, д) неподвижная центроида – горизонтальная прямая, а подвижная – окружность.

В каждый момент времени подвижная и неподвижная центроиды имеют общую точку касания – мгновенный центр скоростей , т.е. точку, скорость которой равна нулю. Поэтому плоское движение можно представить, как качение без скольжения подвижной центроиды по неподвижной.

Задача 11.4.Определить центроиды подвижного звена 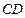антипараллелограмма 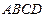, у которого звено закреплено неподвижно, , .

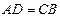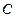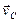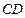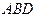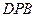Решение.Изобразим в точках и скорости и . Перпендикуляры к ним пересекаются в точке (рис. 11.14) – мгновенном центре скоростей звена . Треугольники и равны по трем сторонам. Следовательно и треугольник равнобедренный. Поэтому

,

.

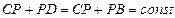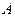Отсюда вытекает, что точка неподвижной плоскости, жестко связанной со звеном , описывает эллипс с фокусами и , а в подвижной плоскости, связанной со звеном 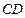, – эллипс с фокусам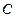и и . Первая кривая является является неподвижной центроидой (она заштрихована), вторая – подвижной.