Задание движения. Углы Эйлера

Движение тела, имеющего одну неподвижную точку, называют иногда сферическим движением или вращением тела вокруг неподвижной точки. Первый термин объясняется тем, что все точки тела движутся по поверхностям сфер, общий центр которых совпадает с неподвижной точкой.

В главе Х мы установили, что твердое тело с одной закрепленной точкой имеет три степени свободы. Три параметра, определяющих положение такого тела относительно неподвижной системы координат (рис. 12.1), можно выбрать различными способами. В теоретической механике положение тела с одной неподвижной точкой, как правило, определяют при помощи углов Эйлера, которые вводятся следующим образом.

Свяжем жестко с телом подвижную систему координат , выбрав начало координат в неподвижной точке (рис. 12.1).

Координатная плоскость пересекается с неподвижной плоскостью вдоль прямой , которая называется линией узлов. Угол, составляемый неподвижной осью 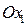с линией узлов, называется углом прецессии и обозначается буквой . Угол, составляемый линией узлов с подвижной осью 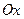, носит название угла собственного вращения и обозначается буквой . Угол между осями и называется углом нутации и обозначается буквой . Все углы отсчитываются соответственно от осе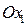й , и против хода часовой стрелки, как показано на рис. 12.1.

Покажем теперь, что зная три функци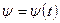и , и 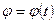, можно всегда найти положение системы координат , а, следовательно, и положение скрепленного с ней тела. Действительно, откладывая от оси 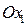угол прецессии , мы найдем линию узлов . Проведем через точку плоскость, перпендикулярную линии узлов, и от оси (эта ось должна лежать в построенной плоскости) отложим угол нутации . Таким образом, будет определено положительное напрвление оси . Через точку проведем плоскость, перпендикулярную оси ; эта плоскость пройдет через линию узлов . Отложим теперь в построенной плоскости от линии узлов угол собственного вращения и определим положительное направление оси 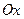. 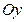Ось должна лежать в той же плоскости и составлять вместе с осям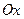и и правую систему координат. Таким образом, углы , и полностью определяют положение осей подвижной системы.

Углы, определяющие положение тела, можно ввести и другим способом. Например, положение корабля относительно его центра тяжести определяется корабельными углами, введенными А.Н. Крыловым. Ось жестко связанной с кораблем системы координат направляется от кормы к носу, ось – к левому борту, ось 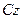расположена в диаметральной плоскости корабля. В положении равновесия корабля оси системы координат совпадают с осями неизменного направления системы координат 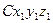. Угол между осью и линией 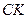, образованной пересечением плоскостей и 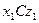, называют углом дифферента. Угол между линией 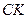и осью называется углом рыскания. Угол 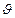между осью 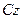и линией 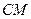пересечения плоскостей и называется углом крена.