
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Под переносным движением будем понимать движение подвижной системы координат относительно неподвижной.
Установление связи между сложным, относительным и переносным движениями позволят решать разнообразные задачи по определению кинематических характеристик сложного и составляющих движений.
В этой главе мы встретимся с необходимостью дифференцирования вектора, определенного в системе координат, которая может двигаться произвольным образом. В связи с этим мы введем понятия абсолютной и относительной производных вектора.
Пусть заданы основная система координат и подвижная система координат, которая совершает произвольное движение. Пусть какой-либо вектор 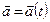 определен в подвижной системе координат, т.е. проекции этого вектора
определен в подвижной системе координат, т.е. проекции этого вектора  на оси подвижной системы – заданные функции времени. Если
на оси подвижной системы – заданные функции времени. Если 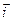 ,
, 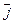 ,
,  – единичные векторы подвижной системы координат, то вектор
– единичные векторы подвижной системы координат, то вектор  может быть представлен в виде
может быть представлен в виде
 . (13.1)
. (13.1)
Установим теперь правило нахождения производной в неподвижной системе координат (абсолютной производной) от этого вектора.
Дифференцируя обе части равенства (13.1) по времени, будем иметь в виду, что векторы 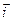 ,
, 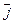 и
и  вследствие движения подвижной системы координат меняют свое направление, т.е. являются функциями времени.
вследствие движения подвижной системы координат меняют свое направление, т.е. являются функциями времени.
Таким образом, абсолютная производная вектора  по времени будет
по времени будет
 . (13.2) Сумма первых трех слагаемых представляет собой производную от вектора
. (13.2) Сумма первых трех слагаемых представляет собой производную от вектора  в подвижной системе координат. В самом деле, если бы мы поставили задачей изучить изменение вектора
в подвижной системе координат. В самом деле, если бы мы поставили задачей изучить изменение вектора  только поотношению к подвижной системе координат, то мы учитывали бы при этом только изменение проекций вектора на оси этой системы координат. Движение же самой системы нас бы не интересовало.
только поотношению к подвижной системе координат, то мы учитывали бы при этом только изменение проекций вектора на оси этой системы координат. Движение же самой системы нас бы не интересовало.
Назовем сумму первых трех слагаемых в (13.2) относительной или локальной производной и обозначим ее через  , т.е.
, т.е.
 . (13.3) Заменяя в формулах (9.11) и (12.10) радиус-вектор
. (13.3) Заменяя в формулах (9.11) и (12.10) радиус-вектор  последовательно на
последовательно на 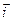 ,
, 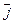 и
и  ; получим
; получим
 ,
,  ,
,  .
.
Поэтому сумма последних трех слагаемых

может быть представлена в виде
 , (13.4) где
, (13.4) где  – угловая скорость подвижной системы координат.
– угловая скорость подвижной системы координат.
Следовательно,
 . (13.5)
. (13.5)
Таким образом, абсолютная производная вектора равна сумме относительной производной этого вектора и векторного произведения угловой скорости подвижной системы координат на этот вектор.
Дата добавления: 2015-04-15; просмотров: 270; Мы поможем в написании вашей работы!; Нарушение авторских прав |