Задача 13.4.

Диск вращается с постоянной угловой скоростью вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. По прямолинейному пазу движется ползун по закону , расстояние от центра диска до паза , . Определить скорость и ускорение ползуна в момент, когда он достигает середины паза .

Решение.Абсолютная скорость ползуна определяется по формуле .

В рассматриваемой задаче подвижная система координат, относительно которой происходит движение ползуна , жестко связывается с диском. Следовательно, переносной скоростью ползуна, когда он совпадает с точкой диска, будет скорость точки диска, т.е.

.

Вектор направлен перпендикулярно .

Относительное движение точки является прямолинейным. Относительная скорость равна

.

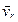Векторы и направлены в одну сторону, следовательно, абсолютная скорость ползуна равна

.

Так как, то момент 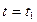прохождения ползуна через точку определится из соотношения 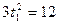, откуда 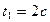и, следовательно, при 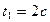имеем

.

Абсолютное ускорение ползуна определяется формулой

.

Диск вращается с постоянной угловой скоростью, поэтому ускорение точки диска (в которой в момент времени находится ползун) равно

.

Вектор направлен к центру диска. Относительное ускорение, как ускорение точки в прямолинейном движении, будет

.

Вектор 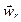направлен вдоль прямой . Так как вектор угловой скорости и вектор 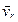взаимно перпендикулярны, то кориолисово ускорение будет равно

и при

.

Направление вектора указано на рис. 13.7.

Абсолютное ускорение ползуна в момент равно

.

Глава XIV