Теорема о сложении скоростей. Выбирая систему координат за основную, предположим, что система координат движется по отношению к основной системе произвольным образом

Выбирая систему координат за основную, предположим, что система координат движется по отношению к основной системе произвольным образом. Движение какой-либо точки 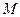может быть изучено как по отношению к основной, так и по отношению к подвижной системе координат методами, изложенными ранее. В данном разделе мы поставим задачу о нахождении связи между скоростями точки по отношению к выбранным нами системам координат. Напомним данные ранее определения (§ 10.2).

Скорость точки 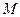по отношению к основной системе координат называется абсолютной скоростью.

Скорость 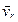точки по отношению к подвижной системе координат называется относительной скоростью.

Важным понятием является понятие о переносной скорости.

Переносной скоростью точки называется скорость той точки подвижной системы координат, с которой в данный момент совпадает движущаяся точка.

Остановимся на этом определении несколько подробнее. Рассматриваемая точка при своем движении относительно подвижного тела, с которым жестко связана подвижная система координат, проходит через разные точки этого тела, имеющие в общем случае отличные друг от друга скорости. Поэтому переносной скоростью точки в данный момент времени будет скорость именно той точки подвижного тела (подвижной системы координат), через которую в данный момент проходит движущаяся точка.

Если радиус-вектор определяет положение точки 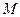по отношению к системе координат , радиус-вектор определяет положение начала системы координат в системе , а радиус-вектор определяет положение точки 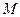в системе координат , то в соответствии с рис. 13.1 имеем

. (13.6)

Пусть координаты точки в подвижной системе координат будут 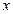, и 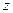. Тогда

,

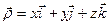где 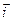, 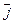и – единичные векторы осей подвижной системы координат.

По определению абсолютная производная радиус-вектора по времени будет абсолютной скоростью точки. Следовательно, дифференцируя равенство (13.6) по времени, найдем абсолютную скорость точки

. (13.7)

Так как вектор определен в подвижной системе координат, то для нахождения абсолютной производной от него воспользуемся формулой (13.5):

, (13.8) где – угловая скорость подвижной системы координат, а

представляет собой относительную производную от по времени. Согласно определению это будет относительная скорость точки, т.е.

. (13.9) Подставляя выражения (13.8) и (13.9) в соотношение (13.7), получим

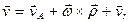, (13.10) где – скорость начала подвижной системы координат по отношению к основной.

Для определения переносной скорости точки закрепим ее в подвижной системе координат, т.е. положим в формуле (13.10) , тогда получим

*. (13.11)

Таким образом, имеем

, (13.12) т.е. абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей.