Мгновенный центр ускорений. Для определения ускорения точки плоской фигуры продифференцируем равенство (11.7) по времени:

Для определения ускорения точки плоской фигуры продифференцируем равенство (11.7) по времени:

.

В этом соотношении , – соответственно ускорения точек и 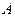, , 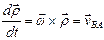– вектор углового ускорения. Вектор , как и вектор 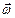, направлен перпендикулярно плоскости фигуры и определен формулой

.

Таким образом, ускорения точек 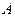и связаны между собой соотношением

. (11.11)

Два последних слагаемых в равенстве (11.11) определяют ускорение точки при закрепленной точке 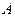. Поэтому их сумма

дает ускорение точки во вращательном движении относительно системы координат .

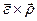При изучении вращательного движения мы уже выяснили, как направлены составляющие вектора ускорения . Легко еще раз укбедиться, пользуясь правилом составления векторного произведения, что имеет направление, совпадпющее с (от точки к полюсу), перпендикулярно . Сохраним за этими составляющими старые названия –осестремительного (или центростремительного) и вращательного ускорений, т.е.

, .

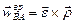Модули этих составляющих будут

, . (11.12)

На рис. геометрически сложены три вектора и определено ускорение точки при помощи формулы

. (11.13)

Таким образом, ускорение любой точки плоской фигуры геометрически складывается из ускорения полюса и осестремительного и вращательных ускорений во вращательном движении тела относительно полюса.

Заметим, что при решении задач, прежде чем строить ускорение точки по формулам (11.13), необходимо вычислить угловую скорость тела, его угловое ускорение и выбрать полюс. За полюс выбирается обычно такая точка, ускорение которой легко находится из условия задачи. Иногда, зная, например, направление искомого ускорения точки, угловое ускорение можно определить по формуле (11.13).

Из (11.12) найдем угол, составленный вектором с направлением на полюс (рис.),

.

Отсюда видно, что этот угол, во-первых не зависит от выбора полюса и, во-вторых, для всех точек при фиксированном времени одинаков.

Модуль ускорения точки при вращении фигуры вокруг полюса также находится из равенства (11.12)

. (11.14) Он зависит от расстояния от точки до полюса.

Введем понятие мгновенного центра ускорений.

Мгновенным центром ускорений называется точка плоской фигуры, ускорение которой в данный момент времени равно нулю.

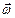Для построения мгновенного центра ускорений будем предполагать, что нам известны ускорение одной из точек , угловая скорость и угловое ускорение , причем предполагается, что 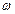и не равны одновременно нулю. Из точки 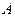отложим под углом к ускорению отрезок

. (11.15)

При этом, если , то отрезок откладывается против хода часовой стрелки, при противоположном знаке – по ходу часовой стрелки.

Убедимся в том, что ускорение точки равно нулю. Выбрав за полюс точку 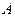, получим

.

Как мы уже отмечали ранее, угол между ускорением точки относительно полюса и направлением на полюс не зависит от выбора полюса. Следовательно, составляет с направлением угол . Такой же угол составляет и с направлением . Поэтому векторы и параллельны. В силу принятого правила отсчета угла ускорения и будут всегда противоположно направлены. Остается теперь установить, что они равны по модулю. Вспоминая (11.14) и подставляя (11.15), получим

.

Отсюда следует:

.

Таким образом, мы доказали, что точка – мгновенный центр ускорений.

Ускорение любой точки в данный момент времени теперь может быть определено так же, как и при вращении вокруг неподвижной оси:

.

(поскольку ).

Следует иметь в виду, что мгновенный центр ускорений и мгновенный центр скоростей, – вообще говоря, разные точки. В этом легко убедиться, рассмотрев простой пример. Допустим, диск катится по горизонтальной плоскости без скольжения и скорость его центра постоянна. Как мы уже знаем, мгновенный центр скоростей находится в точке касания . Так как вектор скорости точки постоянен, то ускорение центра диска равно нулю. Таким образом, мгновенный центр ускорений совпадает с центром диска, а мгновенный центр скоростей – с точкой касания.

Задачи

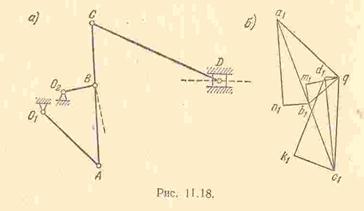Задача 11.5.Две параллельные рейки движутся в разные стороны с постоянными скоростями и . Между рейками зажат диск радиусом , катящийся по рейкам без скольжения. Найти угловую скорость 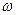диска и скорость его центра 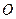, если .

Решение.Так как диск катится по рейкам без скольжения, то скорость его точки , в которой диск соприкасается с верхней рейкой, равна скорости этой рейки . На этом же основании скорость точки диска равна скорости нижней рейки . Так как скорости двух точек и диска параллельны, а сами точки лежат на одном перпендикуляре к скоростям этих точек, то мгновенный центр скоростей диска определится из пропорции

.

С другой стороны,

Решая эти два уравнения совместно, находим

.

Угловая скорость диска

.

Расстояние центра диска от мгновенного центра скоростей

.

Скорость центра диска

.

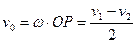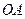Задача 11.6.Кривошип , вращаясь с угловой скоростью вокруг оси неподвижного колеса 1 радиуса , приводит во вращение свободно насаженное на его конце колесо 2 радиуса . Определить угловую скорость колеса 2.

Решение.Сателлит, катясь без скольжения по неподвижному колесу, совершает плоское движение. Положение мгновенного центра скоротей сателлита известно. Он лежит в точке касания колес. Следовательно, для определения угловой скорости сателлита достаточно знать скорость какой-либо одной ее точки. Пользуясь тем, что точка принадлежит не только сателлиту, но и кривошипу 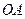/ найдем ее скорость:

.

Тогда

.

Глава XII