Скорости точек при плоском движении

Найдем формулы, позволяющие при заданных функциях (11.1) определить координаты любой точки плоской фигуры.

Пусть система координат является неподвижной системой, а система координат , имеющая начало в произвольно выбранной точке 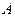плоской фигуры движется поступательно. Систему координат жестко свяжем с плоской фигурой.

Радиус-вектор 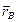, определяющий положение точки относительно неподвижной системы координат , можно задать при помощи двух векторов: 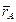, определяющего положение точки 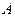в системе отсчета , и 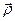, определяющего положение точки в системе отсчета ,

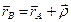. (11.2)

Зная координаты и точки 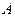и координаты и точки в системе координат , а также угол между осями и , можно определить координаты и точки по формулам:

(11.3)

Напомним, что координаты и – постоянные величины.

Продифференцировав по времени и , найдем проекции скорости точки на координатные оси:

(11.4) К этому же результату можно прийти, дифференцируя непосредственно тождество (11.2),

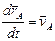. (11.5) Заметим, что , . Что же касается , то это есть скорость точки относительно подвижной системы координат , т.е. относительная скорость (см. § 10.2). Введем для нее обозначение :

.

Движение тела относительно системы координат представляет собой вращение тела вокруг оси , направленной перпендикулярно плоскости чертежа на читателя. Таким образом, скорость есть скорость точки при вращении тела вокруг оси . Для определения этой скорости мы уже получили формулу (§ 10.2)

, где – угловая скорость вращения фигуры вокруг точки 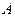(вокруг оси ), которую в дальнейшем будем называть полюсом.

Формула (11.5) принимает теперь вид

, (11.6) т.е. скорость какой-либо точки плоской фигуры равна геометрической сумме скорости полюса 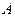и скорости тчки при вращении плоской фигуры вокруг полюса .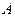

Покажем, что угловая скорость вращения фигуры не зависит от выбора полюса. Пусть 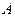и – две какие-нибудь точки плоской фигуры. Пусть полюсу 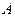соответствует угловая скорость , а плюсу – угловая скорость . Найдем скорость точки , приняв за полюс точку

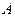
. Приняв теперь за полюс точку , найдем скорость точки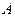

.

Сложив оба равенства, получим

.

Но вектор перпендикулярен плоскости фигуры, и, значит, полученное равенство может выполняться только при . Таким образом, нет надобности в дальнейшем сохранять индекс полюса в обозначении вектора угловой скорости, т.е. .

Формула (11.6) может быть записана теперь в виде

. (11.7)

Если заметить,

, где

, , , то из (11.7) после проектирования на оси координат можно получить уже ранее выписанные формулы (11.4).

Так как , то модуль скорости

,

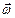ибо вектор перпендикулярен плоскости чертежа. Отметим, что вектор перпендикулярен также . Направление вращения плоской фигуры вокруг полюса зависит только от знака проекции угловой скорости на ось . Так как , то при вращение происходит против хода часовой стренлки и при – по ходу часовой стрелки.

На рис. 11.5, а и б показано, как, зная скорость точки 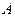, можно найти скорость точки при и .

Из формулы (11.7) следует одна полезная теорема: