Построение движения через задание скорости или ускорения.

Соотношение (1) — это векторный способ задания движения, позволяющий определить положение точки в любой момент времени .

Соотношение (2) — это способ вычисления недостающих кинематических характеристик в этот момент (скорости и ускорения материальной точки) по заданному движению.

Однако движение может быть определено и в том случае, когда задана скорость или ускорение материальной точки.

Действительно, если в любой момент времени задана скорость , то имеем

. (3)

Справа стоит известная вектор-функция . Слева — вектор-функция , определяющая движение точки, является неизвестной.

На формулу (3) можем смотреть, как на уравнение для определения движения. Из него следует, что является первообразной для функции , а потому

= + = + . (4)

Здесь — некоторый постоянный вектор, а = — первообразная функция вектор-функции .

Соотношение (4) задает семейство движений, каждое из которых имеет в любой момент времени заданную скорость .

Чтобы из формулы (4) выделить конкретное движение, проходящее через заданную геометрическую точку с радиус-вектором 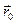при , надо положить в (4) слева и = 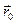. Тогда получим

= + ,

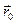где — значение первообразной = в момент .

Выразив отсюда , получим

= + - .

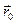Поскольку - = — это определенный интеграл от векторной функции , то можем записать

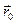= = + . (5)

Формула (5) является векторным заданием движения через задание скорости как функции времени.

Пусть теперь известно ускорение в любой момент времени . Тогда движение будет связано с ним следующим соотношением:

= . (6)

Если учесть, что скорость связана с ускорением (по определению) соотношением

= , (7)

то из (7) мы можем определить скорость по известному вектору . Для этого воспользуемся формулой (5), в которой , , , 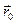заменим соответственно на 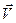, , , 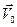; 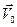обозначает вектор скорости, которую имеет материальная точка в момент времени . Получим

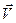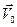= = + . (8)

Учитывая связь (3) скорости с движением , подставим найденную функцию в (5). Тогда найдем вектор-функцию , задающую такое движение материальной точки, которое имеет ускорение, совпадающее в каждый момент времени с заданным ускорением :

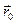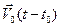= = + + . (9)

На этом движении материальная точка в момент времени проходит через положение 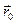и имеет в нем скорость 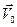. Таким образом, для однозначного построения движения материальной точки по заданному ускорению требуется знать не только положение 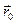в момент , но и скорость .

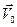Примечание.

Если известна скорость , то, как следует из сказанного, движение определяется из уравнения (3) посредством вычисления интеграла от вектора скорости. В уравнение (3) движение входит через свою производную по времени.

Равенство, в которое входят производные от неизвестной функции, зависящей от одного аргумента, называется обыкновенным дифференциальным уравнением. Порядком уравнения называют наивысший порядок производной от неизвестной функции, с которым эта функция входит в данное уравнение. Сама функция может входить или не входить в него.

Как видим, уравнение (3) является дифференциальным уравнением первого порядка относительно вектор-функции , а уравнение (7) — дифференциальным уравнением второго порядка.

Функция, дифференцируемая в количестве раз, совпадающем с порядком дифференциального уравнения, и обращающая это уравнение в тождество относительно независимой переменной, называется решением данного дифференциального уравнения.

Согласно данному определению, вектор-функция , задаваемая формулами (5) и (9), является решением уравнения (3) и (7), соответственно.

Таким образом, если движение точки задается через скорость или ускорение, то оно строится как решение векторного обыкновенного дифференциального уравнения.

В таких случаях дифференциальное уравнение, решением которого является закон движения материальной точки, называется математической моделью ее движения.