Естественный способ задания движения точки.

1º. Понятие траектории движения.

Пусть движение материальной точки описывается векторным способом

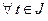, , (1)

где 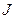— промежуток времени (отрезок или интервал, или полуинтервал), на котором рассматривается движение, 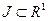, — множество вещественных чисел.

Вектор-функция — вещественная, однозначная, дважды непрерывно дифференцируемая. Соотношение (1) в каждый момент времени задает в евклидовом пространстве 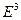геометрическую точку, в которой находится в этот момент движущаяся материальная точка.

Если дополнить пространство 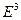четвертым независимым измерением — временной осью , то в этом четырехмерном пространстве уравнение (1) при изменении координаты задает кривую, которая называется графиком движения.

Будем теперь в соотношении (1) смотреть на как на параметр, принимающий значения из промежутка .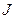

В абсолютном пространстве 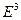построим множество точек , образованное концами векторов при всех значениях этого параметра. За начало векторов при всех будем брать точку отсчета .

Из определений 2 и 3 (см. п.2º, §2 Введения) и определения 1 (см. п.1º, §4 Введения) следует, что множество состоит из положений материальной точки, каждое из которых она может занимать в абсолютном пространстве хотя бы при одном значении времени , совершая движение .