Определение 1. Геометрическое место точек в абсолютном пространстве, состоящее из всех положений материальной точки

Геометрическое место точек в абсолютном пространстве, состоящее из всех положений материальной точки, каждое из которых она может занимать, совершая движение , называется траекторией материальной точки.

Аналитически траектория описывается равенством (1), которое по сути является непрерывным отображением множества 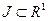вещественной оси на трехмерное евклидово пространство 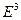. Оно задает в 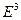однопараметрическое семейство точек, которое в геометрии называется кривой. Таким образом, траектория движения материальной точки — это кривая в трехмерном евклидовом пространстве. В отличие от графика движения, который строится в четырехмерном пространстве, где четвертой координатой служит время , траектория строится в трехмерном пространстве и является проекцией графика движения на абсолютное пространство .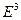

Траектория отличается от графика движения еще и тем, что график движения — всегда самонепересекающаяся кривая, а траектория может быть как самонепересекающейся, так и самопересекающейся и (или) замкнутой.

Соотношение (1) дает векторное описание траектории. Если в пространстве 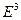фиксирована система отсчета , то траектория движения определяется в координатной форме тремя равенствами

, , , ,

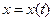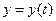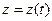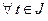где 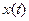, , 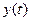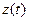— координатные функции вектор-функции .

Пример.

Пусть точка совершает движение в плоскости 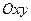на промежутке времени 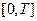по закону

, , .

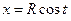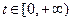Графиком ее движения, очевидно, будет являться винтовая линия на цилиндре радиуса 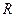с осью, совпадающей с координатной осью изменения времени (см. рис.1).

Траекторией движения является окружность радиуса 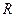в плоскости 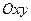(см. рис.2). Стрелками указано направление движения точки по этой траектории при возрастании .

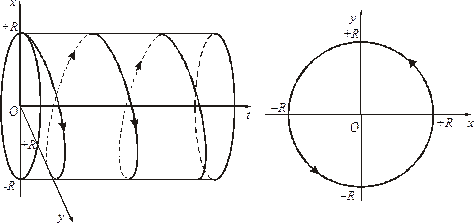
Рис. 1. Рис.2.

В механике для любой вектор-функции , заданной и непрерывной на некотором промежутке времени 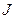, вводится понятие ее годографа.