Ordm;. Описание естественного способа задания движения.

Суть естественного способа задания движения материальной точки состоит в следующем:

– задается регулярная кривая не ниже второй кратности (без особых точек)

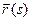= ; (5)

– задается закон движения по этой кривой

, (6)

где 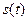— дважды непрерывно дифференцируемая функция от .

Установим связь естественного способа задания движения с векторным. Подставим (6) в (5). Получим

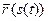= . (7)

Соотношение (7) — это векторный способ задания движения.

Установим обратную связь. Пусть движение материальной точки задается векторным способом

= , . (8)

Дадим алгоритм перехода к естественному способу.

Будем смотреть на соотношение (8) как на векторное задание кривой в абсолютном пространстве. В нем является параметром, принимающим значения из промежутка 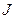, а вектор-функция – параметризацией кривой. По определению, данная кривая является траекторией движения.

При естественном способе требуется, чтобы траектория задавалась в естественной параметризации .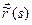

Поскольку параметризация , вообще говоря, не является естественной для данной траектории, то алгоритм перехода от векторного способа к естественному должен содержать описание действий, направленных на построение естественной параметризации .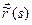

Чтобы определить функцию 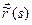, достаточно найти связь 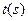между длиной дуги 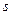траектории и временем . Если такая связь будет найдена, то, заменив в правой части равенства (8) аргумент на 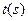, получим естественную параметризацию .

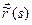Зависимость 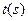может быть найдена из закона движения как обратная функция по отношению к нему. Этот закон 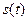, как и естественная параметризация траектории, должен быть известен при естественном способе задания движения. А потому задача перехода от векторного способа к естественному будет решена, если укажем алгоритм построения 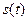по вектор-функции .

Поставленную задачу будем решать при следующем ограничении на (только при его выполнении возможен переход к естественному способу):

– траектория, определяемая заданием (8), является регулярной кривой второй кратности и без особых точек.

Установим вид функции 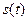, соответствующей движению . Для этого выполним следующие операции:

– находим 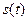, используя формулу для дифференциала дуги , а именно, фиксируем и интегрируем данное соотношение в пределах от до ; в результате получим искомую функцию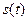

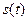= , ; (9)

очевидно, 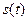является неубывающей, так как под интегралом стоит неотрицательная функция ;

– находим обратную функцию к функции , задаваемой формулой (9),

; (10)

такая функция 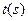существует, по крайней мере, для всех , при которых , т.е. при тех , где 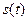строго монотонно возрастает;

– подставим (10) в (8); в совокупности с (9) будем иметь

= , .

Таким образом, приходим к естественному способу задания движения.