Замечание 2.

Если в формуле (9) окажется, что 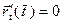при каких-то значениях 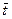, то подбираем новую параметризацию 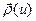, в которой параметр 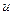связан со временем соотношением

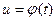, (11)

допускающим однозначное и дважды непрерывно дифференцируемое обращение 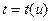. Основное требование к указанной параметризации следующее:

вектор-функция

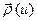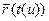= (12)

должна иметь значение 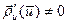при .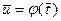

Поскольку траектория движения является регулярной кривой без особых точек, то параметризация 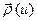существует. Данное утверждение следует из того, что для таких кривых всегда существует естественная параметризация 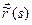. А в естественной параметризации при всех значениях длины дуги 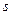выполняется равенство

.

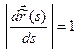После построения параметризации 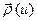функцию находим путем обращения функции 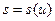, где 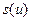имеет следующую зависимость от :

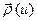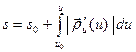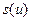= . (13)

Соотношение (13) выводится по той же схеме, по которой получено (9).

Так как функция 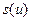, определяемая по формуле (13), обладает свойством = 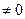, то в окрестности точки 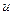= , 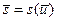она допускает обращение

. (14)

Подстановка функции (14) в соотношение (12) и функции (11) в (13) дает окончательно = , 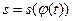— естественный способ задания движения.

4º. Вычисление скорости и ускорения при естественном способе
задания движения.

По определению скорости материальной точки можем записать 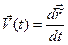. Здесь 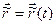– движение точки , заданное векторным способом; – ее скорость в момент времени .

Согласно связи векторного способа с естественным имеем = 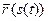, где 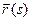– естественная параметризация траектории движения, а 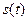– закон движения по этой траектории. Дифференцируя 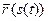по , получаем

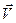= , (15)

где 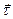— орт касательной к траектории в той ее точке, с которой совпадает положение материальной точки в момент времени .

Из (15) можем сделать следующие заключения:

а) скорость параллельна 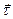— орту касательной к траектории в том

положении точки , которое она занимает в момент времени ;

б) = .

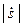Обратимся теперь к выводу формулы для вычисления ускорения 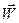материальной точки. По определению имеем 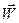= 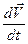. Подставляя правую часть (15) вместо 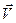и дифференцируя по , получим

= = + = + .

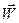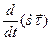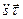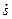
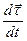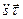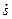
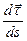
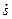Воспользуемся формулой Френ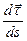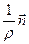е = = , где 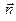– орт главной нормали к траектории в том положении, которое занимает на ней точка в момент времени ; – кривизна, а – радиус кривизны траектории в этом положении. Тогда выражение для 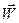примет вид:

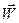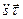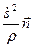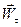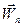= + = + . (16)

Вектор 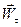= 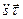называется касательным (тангенциальным) ускорением точки , а вектор 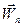= = 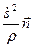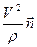– ее нормальным ускорением.

Величина скорости обозначена 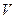= = 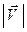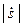. Формула (16) составляет предмет теоремы Гюйгенса.