Ordm;. Скорость и ускорение точки в круговом движении.

Построим явные зависимости ортов 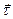и 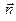репера Френе от радиуса 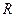и длины дуги 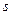на круговом движении. Согласно формулам Френе, имеем

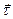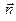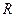
= , = = , (10)

где 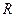— радиус кривизны. Здесь воспользовались известным соотношением = 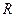для окружности. Отсюда после подстановки (6),(7) в формулу для 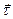находим

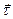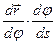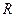
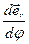
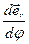= = = . (11)

Далее, введя обозначение = 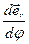и подставляя в него (6), получим зависимость орта от угла в следующем виде: =- + .

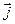
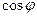А тогда, учитывая равенства (11) и (7), окончательно для орта 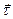будем иметь

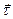= . (12)

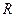Зависимость орта от и 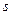получим, подставив орт 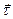из (12) во вторую формулу Френе (10). После дифференцирования по 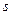выражение для вектора 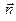примет вид

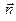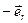= = . (13)

Дадим теперь выражения для скорости 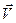и ускорения 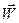в круговом движении. Согласно выводам §2, скорость 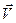и ускорение 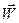будут вычисляться по формулам

= = , = + ,

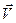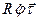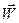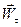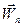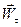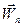где = = — касательное ускорение, = = — нормальное ускорение.

Введем обозначения = , = = . Тогда выражения для векторов 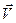, , 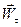, 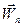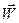и их модулей примут следующий вид:

= , = = ;

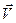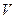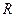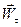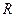= , = = ; (14)

= , = = ,

, .

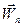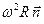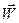
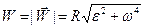Если введем векторы

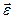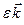= , = = = , = = = = , (15)

то через них скорость 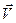и ускорение 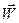точки в круговом движении можем записать в следующей форме:

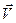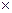
= , (16)

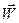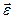
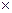
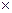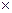
= + ( ). (17)

Соотношение (16) называется формулой Эйлера для кругового движения материальной точки.

Соотношение (17) называется формулой Ривальса для ускорения материальной точки в круговом движении.

Справедливость формул (16),(17) легко устанавливается, если подставить в их левые части соотношения (14) для 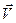и 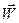, а в правые — соотношения (15),(12),(13) и учесть очевидные равенства

, , ,

которые выполняются на кругового движении.

Для векторов , , 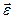приняты следующие названия:

— вектор углового поворота точки в круговом движении;

— вектор мгновенной угловой скорости кругового движения точки;

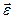— вектор мгновенного углового ускорения в круговом движении

точки.

Из (15) следует, что в любой момент времени вектора , и 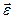ортогональны плоскости движения материальной точки.