Ordm;. Задание движения в полярных координатах.

Задать движение в полярных координатах — это значит задать закон изменения координат и по времени

= , = (3)

в вектор-функции , определяющей связь положения точки с полярными координатами и . Эта связь в векторной форме имеет вид

.

Введем орты 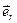и 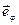, вычисляемые через полярные координаты точки . Положим, по определению,

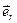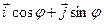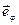
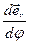= = , = , (4)

где .

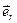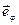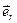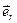Очевидно, — это орт радиус-вектора точки , — орт, характеризующий изменение направления орта при изменении угла . Иначе, это орт касательной к окружности радиуса с центром в точке (касательной в точке ). Орты и 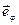взаимно ортогональны.

Векторы 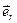и 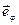называются базисом полярной системы координат.

Используя закон движения (3) и первое соотношение в (4), получим

= = . (5)

Формула (5) — это векторный способ задания движения через полярные координаты. В ней

= .