
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм построения радиуса кривизны кривой.
Пусть кривая задается параметрически:
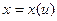 ,
, 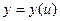 ,
, 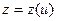 ,
, 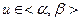 . (18)
. (18)
1). Задаем какое-либо движение по кривой:  . Например, в качестве
. Например, в качестве  берем функцию
берем функцию  .
.
2). Вычислим величины  и
и 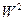 . Очевидно, можем записать:
. Очевидно, можем записать:
 =
= 
 ,
,  =
= 
 ,
, 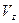 =
= 
 .
.
Здесь  ,
,  ,
, 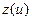 — заданные функции (18). Отсюда получаем формулу для вычисления величины
— заданные функции (18). Отсюда получаем формулу для вычисления величины  , стоящей в правой части соотношения (17),
, стоящей в правой части соотношения (17),  =
=  .
.
Аналогично, имеем
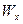 =
=  =
=  ,
, 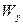 =
=  =
=  ,
, 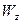 =
=  =
=  .
.
По формуле 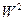 =
=  , подставляя соотношения (18), находим величину
, подставляя соотношения (18), находим величину 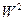 , стоящую под корнем в правой части выражения (17).
, стоящую под корнем в правой части выражения (17).
3). Вычислим величину  . Формулу для ее расчета получаем через последовательность следующих очевидных соотношений
. Формулу для ее расчета получаем через последовательность следующих очевидных соотношений
 =
=  =
=  =
=  =
=  .
.
4). Подставляя в выражение для радиуса кривизны (17)
 =
= 
вычисленные значения  ,
, 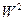 ,
,  , получим требуемое.
, получим требуемое.
Применение алгоритма рассмотрим на примере вычисления радиуса кривизны эллипса в любой его точке.
Уравнение эллипса в декартовых координатах имеет вид:
 .
.
Переходим к параметрическому уравнению эллипса:  ,
,  .
.
Задаем закон движения по эллипсу:  . Тогда
. Тогда
1).  =
=  =
=  ,
,  =
=  =
=  ,
,  .
.
2). 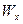 =
=  ,
, 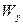 =
=  ,
, 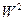 =
=  .
.
3).  =
=  (
( 
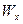 +
+ 
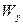 )
)  (
(  )
) 
 .
.
Подставляя  ,
, 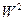 и
и  =
=  в (17), получим формулу для вычисления радиуса кривизны эллипса в любой его точке
в (17), получим формулу для вычисления радиуса кривизны эллипса в любой его точке
 =
=  =
=  .
.
В декартовых координатах она будет иметь вид
 =
=  . (19)
. (19)
В частности, если  , то эллипс вырождается в окружность. Тогда
, то эллипс вырождается в окружность. Тогда  , и из (19) получим
, и из (19) получим  =
=  в любой точке окружности.
в любой точке окружности.
Пусть  . Вычисляем
. Вычисляем  в вершинах эллипса. В вершинах на оси
в вершинах эллипса. В вершинах на оси 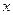 имеем
имеем  . Для них из (19) получим
. Для них из (19) получим
 =
=  .
.
В вершинах на оси 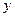 имеем
имеем  . Из (19) следует, что в них
. Из (19) следует, что в них
 =
=  .
.
Дата добавления: 2015-04-15; просмотров: 283; Мы поможем в написании вашей работы!; Нарушение авторских прав |