
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Некоторые понятия из дифференциальной геометрии.
Пусть дана кривая 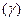 . На этой кривой будем обозначать
. На этой кривой будем обозначать  — некоторую фиксированную точку и
— некоторую фиксированную точку и  — произвольную точку.
— произвольную точку.
Определение 3.
Кривая 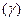 называется регулярной степени
называется регулярной степени  кривой, если существует параметризация
кривой, если существует параметризация  такая, что вектор-функция
такая, что вектор-функция  будет
будет  раз непрерывно дифференцируема, и
раз непрерывно дифференцируема, и 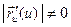 в любой точке кривой. Здесь
в любой точке кривой. Здесь
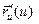 =
=  .
.
Если  =1, то кривая называется гладкой.
=1, то кривая называется гладкой.
Определение 4.
Точка  кривой называется особой, если для любой параметризации
кривой называется особой, если для любой параметризации  в точке
в точке  выполняется равенство
выполняется равенство  .
.
Определение 5.
Предельное положение хорды  (если оно существует), когда точка
(если оно существует), когда точка  стремится к точке
стремится к точке  (по кривой), называется касательной прямой в точке
(по кривой), называется касательной прямой в точке  к кривой
к кривой 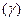 .
.

Рис.3.
На рисунке 3 обозначены:
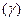 – заданная кривая;
– заданная кривая;
 – фиксированная точка на кривой
– фиксированная точка на кривой 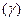 ;
;
 – переменная точка на кривой
– переменная точка на кривой 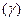 ;
;
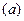 – касательная прямая в точке
– касательная прямая в точке  ;
;
 – точка отсчета в пространстве;
– точка отсчета в пространстве;
 – положение точки
– положение точки  относительно точки
относительно точки  ;
;
 – положение точки
– положение точки  относительно точки
относительно точки  ;
;
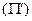 – плоскость, проходящая через касательную
– плоскость, проходящая через касательную 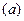 и хорду
и хорду  .
.
Определение 6.
Нормалью в точке  к кривой
к кривой 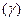 называется любая прямая, перпендикулярная к касательной в точке
называется любая прямая, перпендикулярная к касательной в точке  .
.
Определение 7.
Плоскость, перпендикулярная к касательной в точке  , называется нормальной плоскостью в точке
, называется нормальной плоскостью в точке  (см. рис.4).
(см. рис.4).
Пусть 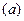 — касательная в точке
— касательная в точке  к кривой
к кривой 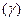 . Проведем плоскость
. Проведем плоскость 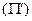 через касательную
через касательную 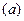 и хорду
и хорду  (см. рис.3).
(см. рис.3).
Определение 8.
Предельное положение плоскости (  ) при
) при  —>
—>  (если оно существует) называется соприкасающейся плоскостью.
(если оно существует) называется соприкасающейся плоскостью.
Вдифференциальной геометрии доказано, что если можно указать параметризацию кривой  такую, что существуют
такую, что существуют 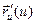 и
и  в точке
в точке  , и при этом
, и при этом 
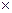

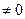 , то в точке
, то в точке  существует соприкасающаяся плоскость, и нормаль к этой плоскости коллинеарна вектору
существует соприкасающаяся плоскость, и нормаль к этой плоскости коллинеарна вектору
 .
.
Здесь штрихом обозначена производная по 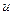 , а
, а  — значение параметра, соответствующее точке
— значение параметра, соответствующее точке  .
.
Определение 9.
Главной нормалью в точке  называется линия пересечения нормальной и соприкасающейся плоскостей. Иначе, главная нормаль — это нормаль, лежащая в соприкасающейся плоскости (см. рис.4).
называется линия пересечения нормальной и соприкасающейся плоскостей. Иначе, главная нормаль — это нормаль, лежащая в соприкасающейся плоскости (см. рис.4).
 — главная нормаль
— главная нормаль
 |
 нормальная плоскость
нормальная плоскость

соприкасающаяся
 плоскость
плоскость
 |


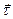 — касательная
— касательная
 | |||
 |
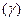
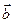 — бинормаль спрямляющая плоскость
— бинормаль спрямляющая плоскость
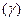
Рис.4.
Определение 10.
Бинормаль в точке  — это прямая, перпендикулярная соприкасающейся плоскости в точке
— это прямая, перпендикулярная соприкасающейся плоскости в точке  (см. рис.4).
(см. рис.4).
Определение 11.
Спрямляющей плоскостью в точке  называется плоскость, перпендикулярная главной нормали в точке
называется плоскость, перпендикулярная главной нормали в точке  (см. рис.4).
(см. рис.4).
Очевидно, спрямляющая плоскость проходит через касательную прямую и бинормаль в точке  .
.
Определение 12.
Естественным трехгранником в точке  называется трехгранник, образованный нормальной, соприкасающейся и спрямляющей плоскостями точки
называется трехгранник, образованный нормальной, соприкасающейся и спрямляющей плоскостями точки  (см. рис.4).
(см. рис.4).
Определение 13.
Длиной дуги кривой называется предел, к которому стремится периметр ломаной, вписанной в дугу, когда количество звеньев стремится к бесконечности, а максимальная длина звена стремится к нулю.
Дифференциал дуги кривой  связан с параметризацией
связан с параметризацией  кривой следующей зависимостью
кривой следующей зависимостью
 =
=  =
=  . (4)
. (4)
Здесь  .
.
Формула для  справедлива в декартовой прямоугольной системе координат. В аффинной системе она имеет вид
справедлива в декартовой прямоугольной системе координат. В аффинной системе она имеет вид
 =
=  =
=  =
= 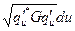 =
=  .
.
Определение 14.
Параметризация называется естественной, если в качестве параметра при задании кривой выступает 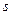 — длина дуги кривой, исчисляемая от некоторой фиксированной точки на этой кривой.
— длина дуги кривой, исчисляемая от некоторой фиксированной точки на этой кривой.
Справедливо утверждение: для регулярной кривой (т.е. кривой без особых точек) всегда имеет место неравенство  для любого
для любого 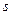 .
.
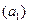


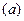
 |






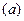
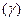
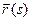

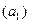
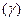
 Рис.5.
Рис.5.
Иначе говоря, регулярная кривая в естественной параметризации при любых 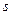 имеет значения
имеет значения  . Более того, из (4) следует, что
. Более того, из (4) следует, что  .
.
Обозначим через 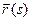 и
и  положения точек
положения точек  и
и  на кривой
на кривой  (см. рис.5). Проведем касательные
(см. рис.5). Проведем касательные 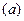 и
и 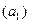 к ней в этих точках. Угол
к ней в этих точках. Угол  , образованный касательными, называется углом смежности.
, образованный касательными, называется углом смежности.
Определение 15.
Если существует предел  , то он называется кривизной кривой
, то он называется кривизной кривой 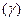 в точке
в точке  .
.
Очевидно, кривизна  кривой
кривой 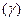 всегда неотрицательна, т.е.
всегда неотрицательна, т.е.  .
.
В дифференциальной геометрии доказано, что если кривая задается в параметризации  , то в любой неособой точке, где существуют
, то в любой неособой точке, где существуют  и
и  , кривизна кривой может быть вычислена по формуле
, кривизна кривой может быть вычислена по формуле 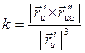 .
.
Если кривая задается в естественной параметризации, то  .
.
Определение 16.
Величина  называется радиусом кривизны кривой в точке
называется радиусом кривизны кривой в точке  .
.
Здесь  — кривизна кривой в точке
— кривизна кривой в точке  .
.
Справедливы следующие формулы Френе, устанавливающие связь направляющих ортов касательной, главной нормали и бинормали с естественной параметризацией кривой:
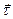 =
=  — орт, коллинеарный касательной в точке
— орт, коллинеарный касательной в точке  ;
;
 =
= 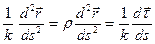 — орт, коллинеарный главной нормали в точке
— орт, коллинеарный главной нормали в точке  ,
,
или отсюда 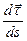 =
=  =
= 
 ;
;
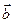 =
= 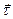
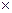
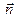 — орт, коллинеарный бинормали в точке
— орт, коллинеарный бинормали в точке  .
.
Векторы 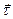 ,
,  ,
, 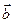 являются взаимно ортогональными единичными векторами и образуют правую тройку.
являются взаимно ортогональными единичными векторами и образуют правую тройку.
Определение 17.
Тройка векторов 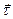 ,
,  ,
, 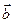 с началом в точке
с началом в точке  называется репером Френе.
называется репером Френе.
Определение 18.
Естественной системой координат называется декартовая прямоугольная система координат с полюсом в выбранной точке  на кривой и базисом, совпадающим с репером Френе в этой точке.
на кривой и базисом, совпадающим с репером Френе в этой точке.
Дата добавления: 2015-04-15; просмотров: 251; Мы поможем в написании вашей работы!; Нарушение авторских прав |