
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Связь векторного и координатного способов.
Пусть движениеточки задается координатным способом. Тогда формулы (13) и (15) определяют вектор-функцию  , которая является основой для векторного способа задания движения.
, которая является основой для векторного способа задания движения.
Пусть движениеточки задается векторным способом. Тогда из (13) и (15) можем получить координатный способ задания движения, если вычислим координаты вектор-функции  . Если системой отсчета является система
. Если системой отсчета является система  , то, умножая (13) скалярно на
, то, умножая (13) скалярно на  ,
, 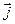 ,
,  последовательно, получим
последовательно, получим
 ,
, 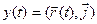 ,
, 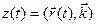 .
.
Здесь 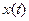 ,
, 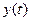 ,
, 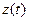 — координаты точки, вычисленные по ее заданному положению
— координаты точки, вычисленные по ее заданному положению  в любой момент времени
в любой момент времени  . Как видно из этих выражений, геометрические координаты точки в любой момент времени
. Как видно из этих выражений, геометрические координаты точки в любой момент времени  равны ортогональным проекциям вектор-функции
равны ортогональным проекциям вектор-функции  на оси системы отсчета
на оси системы отсчета  в момент времени
в момент времени  .
.
Аналогично, если система отсчета является аффинной 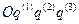 , то, умножая (15) последовательно скалярно на векторы
, то, умножая (15) последовательно скалярно на векторы 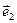
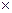
 ,
, 
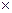
 ,
, 
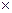
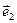 , получим
, получим 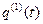
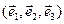 =
= 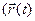 ,
, 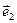 ,
,  .
.
Отсюда
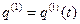
 , (19)
, (19)
где введено обозначение 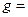
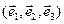 .
.
Замечание.
Легко показать, что 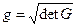 , если система координат правая;
, если система координат правая;  , если эта система левая.
, если эта система левая.
Аналогично (при умножении на ( 
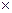
 ) и на (
) и на ( 
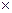
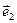 )), получим
)), получим
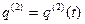
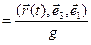 , (20)
, (20)
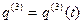
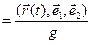 . (21)
. (21)
Таким образом находятся координаты 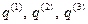 точки
точки  в аффинной системе при известном векторе
в аффинной системе при известном векторе  .
.
Примечание.
Выражения (20) и (21) легко можно записать, зная формулу (19). Обозначим последовательность индексов у переменных 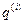 ,
, 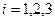 в виде
в виде
1 —> 2 —> 3 —> 1 (22)
и последовательность индексов у ортов 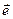 также в виде
также в виде
1 —> 2 —> 3 —> 1. (23)
Тогда соотношение (20) получается из (19) заменой в равенстве (19) индекса «1» при 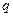 на следующий за ним в последовательности (22) индекс «2», и заменой индексов «2» и «3» у ортов
на следующий за ним в последовательности (22) индекс «2», и заменой индексов «2» и «3» у ортов 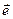 на следующие за ними в последовательности (23) индексы «3» и «1».
на следующие за ними в последовательности (23) индексы «3» и «1».
После записи выражения (20) соотношение (21) строится аналогичным образом из (20) по правилу замены индексов при 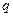 и
и 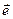 согласно схемам (22) и (23).
согласно схемам (22) и (23).
Если две или более формулы выводятся последовательно друг из друга заменой переменных и (или) индексов на их другие значения из заданных упорядоченных последовательностей, то говорят, что последовательность формул строится по правилу круговой перестановки заданных переменных и (или) индексов.
Таким образом, согласно данной формулировке можно сказать, что последовательность формул (19),(20),(21) строится круговой перестановкой переменных 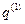 —>
—> 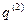 —>
—>  —>
—> 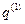
и ортов  —>
—> 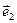 —>
—>  —>
—>  ,
,
или, иначе, — круговой перестановкой индексов 1—>2—>3—>1 у переменных 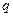 и ортов
и ортов 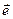 .
.
Дата добавления: 2015-04-15; просмотров: 317; Мы поможем в написании вашей работы!; Нарушение авторских прав |