
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Описание координатного способа задания движения.
Зафиксируем в пространстве точку отсчета  и систему отсчета. Если в качестве системы отсчета выбрана декартовая прямоугольная система координат, то, как отмечено во Введении, она будет обозначаться
и систему отсчета. Если в качестве системы отсчета выбрана декартовая прямоугольная система координат, то, как отмечено во Введении, она будет обозначаться 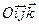 или
или  , где
, где  ,
, 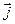 ,
,  — базис, а
— базис, а 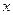 ,
, 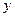 ,
, 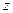 — координаты точек в ней.
— координаты точек в ней.
Если в качестве системы отсчета принимается аффинная система координат, то будем обозначать ее 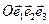 или
или 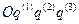 , где
, где  ,
, 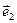 ,
,  — базис, а
— базис, а 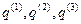 — координаты точек. При выборе системы
— координаты точек. При выборе системы 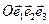 считается известной (задается) также матрица метрических коэффициентов
считается известной (задается) также матрица метрических коэффициентов  , где
, где 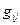 =
=  ,
,  .
.
Напомним определения из векторной алгебры.
Определение 1.
Координатами вектора 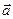 в заданной системе отсчета называются коэффициенты в разложении вектора
в заданной системе отсчета называются коэффициенты в разложении вектора 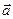 по базисным векторам.
по базисным векторам.
Из определения следует, что если обозначить 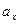 ,
, 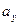 ,
,  — координаты вектора
— координаты вектора 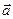 в декартовой системе
в декартовой системе  , а
, а 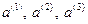 — координаты этого же вектора
— координаты этого же вектора 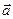 в аффинной системе
в аффинной системе 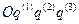 , то можем записать
, то можем записать
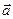 =
=  ,
, 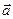 =
= 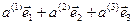 .
.
Определение 2.
Координаты радиус-вектора  точки
точки  относительно точки отсчета
относительно точки отсчета  в заданной системе отсчета называются координатами этой точки
в заданной системе отсчета называются координатами этой точки  в указанной системе отсчета.
в указанной системе отсчета.
Согласно определению 2 с учетом принятых обозначений координат точки в системах отсчета 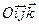 и
и 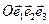 можем записать
можем записать
 =
=  , (10)
, (10)

 . (11)
. (11)
Если задать в каждый момент времени  координаты
координаты 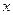 ,
, 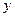 ,
, 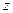 точки
точки  в виде дважды непрерывно дифференцируемых функций
в виде дважды непрерывно дифференцируемых функций 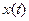 ,
, 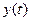 ,
, 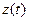 , то будем иметь
, то будем иметь
 ,
, 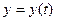 ,
, 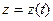 . (12)
. (12)
Тогда, подставляя (12) в (10), получим
 =
=  =
=  . (13)
. (13)
Соотношение (13) позволяет определить положение точки  в любой момент
в любой момент  из промежутка времени, где заданы правые части равенств (12). Причем, поскольку функции
из промежутка времени, где заданы правые части равенств (12). Причем, поскольку функции 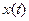 ,
, 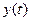 ,
, 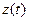 дважды непрерывно дифференцируемы, то вектор-функция
дважды непрерывно дифференцируемы, то вектор-функция  , связанная с ними равенством (13), будет также дважды непрерывно дифференцируема. А это значит, что (12) задают движение материальной точки.
, связанная с ними равенством (13), будет также дважды непрерывно дифференцируема. А это значит, что (12) задают движение материальной точки.
Аналогично, задавая в каждый момент времени  аффинные координаты
аффинные координаты 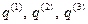 точки
точки  в виде дважды непрерывно дифференцируемых функций
в виде дважды непрерывно дифференцируемых функций 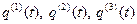 , будем иметь
, будем иметь
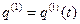 ,
, 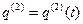 ,
,  . (14)
. (14)
Подставляя (14) в (11), получим, что положение  точки
точки  в любой момент времени
в любой момент времени  может быть вычислено по формуле
может быть вычислено по формуле

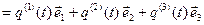 , (15)
, (15)
которая так же, как и (13), определяет движение точки  .
.
Способ задания движения материальной точки по формуле (12) или (14) называется координатным.
Для этого способа, в отличие от векторного, существенным является выбор системы отсчета (выбор системы координат), в которой дается описание движения.
2.2. Вычисление скорости и ускорения при координатном способе
задания движения.
По определению скорости точки  имеем
имеем
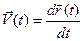 , (16)
, (16)
где  — вектор-функция, задающая движение этой точки.
— вектор-функция, задающая движение этой точки.
При координатном способе задания движения вектор-функция  через координатные функции
через координатные функции 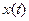 ,
, 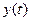 ,
, 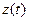 вычисляется по формуле (13) либо через координатные функции
вычисляется по формуле (13) либо через координатные функции 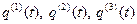 по формуле (15).
по формуле (15).
Поэтому из (13) и (15) будем иметь, соответственно,
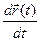 =
= 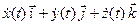 ,
, 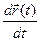
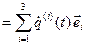 .
.
Таким образом, подставляя 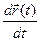 в (16), получим следующие выражения для скорости
в (16), получим следующие выражения для скорости  :
:
– при задании движения в декартовых координатах 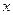 ,
, 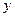 ,
, 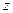 это выражение примет вид
это выражение примет вид
 =
= 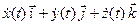 ; (17)
; (17)
– при задании движения в аффинных координатах 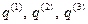 , соответственно, будем иметь
, соответственно, будем иметь

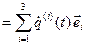 . (18)
. (18)
Обозначим  ,
,  ,
, 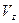 — координаты вектора
— координаты вектора 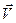 в системе отсчета
в системе отсчета  , а
, а  — координаты вектора
— координаты вектора 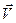 в аффинной системе
в аффинной системе 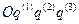 . Тогда по определению координат вектора можем записать
. Тогда по определению координат вектора можем записать
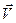 =
=  ,
, 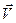
 .
.
Сопоставляя эти соотношения с (17),(18), видим, что в момент времени  координаты скорости
координаты скорости 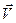 совпадают с производными от координат вектора
совпадают с производными от координат вектора  в системе
в системе  , если движение задается декартовыми координатами и с производными от координат вектора
, если движение задается декартовыми координатами и с производными от координат вектора  в системе
в системе 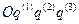 , если движение задается аффинными координатами:
, если движение задается аффинными координатами:
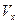 =
=  ,
,  =
= 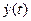 ,
, 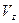 =
=  ;
;

 ,
, 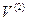
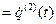 ,
, 
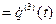 .
.
Геометрически координаты вектора скорости  можем получить путем совмещения начала вектор-функции
можем получить путем совмещения начала вектор-функции 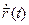 с точкой отсчета
с точкой отсчета  и проектирования конца вектора
и проектирования конца вектора 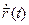 на соответствующие координатные оси.
на соответствующие координатные оси.
Для вычисления ускорения точки действуем аналогично. Учитывая, что по определению ускорения 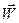 точки имеем
точки имеем
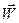 =
=  =
=  ,
,
получим:
– при задании движения в декартовых координатах 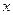 ,
, 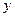 ,
, 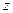 выполняются равенства
выполняются равенства
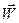 =
=  =
= 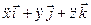 ;
;
– при задании движения в аффинных координатах 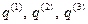 эти равенства приобретают вид
эти равенства приобретают вид
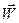
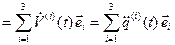 .
.
Если обозначим 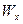 ,
, 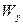 ,
, 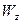 — декартовые координаты вектора
— декартовые координаты вектора 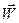 , а
, а 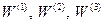 — его аффинные координаты, то связь
— его аффинные координаты, то связь 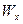 ,
, 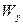 ,
, 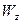 со вторыми производными от заданных координатных функций
со вторыми производными от заданных координатных функций 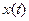 ,
, 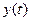 ,
, 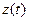 ,
, 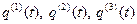 будет такова:
будет такова:
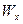 =
=  ,
, 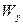 =
=  ,
, 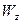 =
= 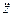 ;
;  .
.
Из полученных выражений для 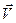 и
и 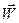 легко выписываются формулы для вычисления модуля скорости и модуля ускорения, а также для направляющих косинусов этих векторов.
легко выписываются формулы для вычисления модуля скорости и модуля ускорения, а также для направляющих косинусов этих векторов.
Для 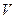 =
= 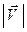 и
и 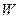 =
= 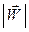 будем иметь:
будем иметь:
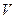 =
= 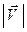 =
= 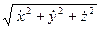 =
= 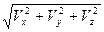 ;
; 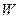 =
= 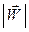 =
= 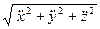 =
=  .
.
Для направляющих косинусов  ,
, 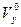 ,
, 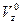 вектора скорости
вектора скорости 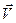 имеем:
имеем:
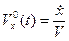 ,
, 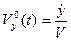 ,
, 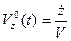 .
.
Аналогично, для направляющих косинусов 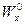 ,
,  ,
,  вектора ускорения
вектора ускорения 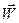 :
:  ,
, 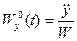 ,
, 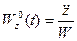 .
.
В аффинной системе координат формула для вычисления модуля скорости 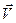 может быть получена из следующих соотношений:
может быть получена из следующих соотношений:
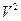 =
= 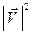 =
= 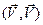

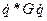 ,
,
где введены обозначения
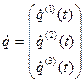 — вектор-столбец, составленный из производных от
— вектор-столбец, составленный из производных от
заданных координатных функций 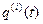 ,
, 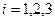 ;
;
 — матрица метрических коэффициентов аффинной системы
— матрица метрических коэффициентов аффинной системы
координат;
символ 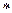 обозначает операцию транспонирования.
обозначает операцию транспонирования.
Аналогично, для 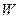 =
= 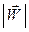 получим
получим 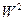 =
=  =
=  =
=  .
.
Здесь  — вектор-столбец, составленный из вторых производных от заданных координатных функций
— вектор-столбец, составленный из вторых производных от заданных координатных функций 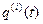 ,
, 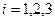 .
.
Дата добавления: 2015-04-15; просмотров: 252; Мы поможем в написании вашей работы!; Нарушение авторских прав |