Определение 2.

Годографом вектор-функции называется геометрическое место точек в абсолютном пространстве, образованное концами векторов , имеющих своим началом точку отсчета .

Очевидно, годограф вектор-функции , задающей движение, совпадает с траекторией движения точки.

Понятие годографа чаще всего применяется к скорости движения точки (называется годографом скорости) и к ее ускорению (годограф ускорения).

Если известна скорость материальной точки при всех , то для построения еегодографа следует параллельным переносом совместить начало вектора скорости точки с точкой отсчета в каждый момент времени . Тогда геометрическое место концов построенного таким образом множества векторов при всех будет являться годографом вектора скорости точки . Аналогично строится годограф ускорения этой точки.

Параметрически годограф скорости в трехмерном пространстве задается уравнениями

где — координаты точек годографа скорости, а 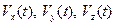— координаты скорости материальной точки.

Аналогично для годографа ускорения параметрические уравнения имеют вид

где — координаты точек годографа ускорения, а — координаты ускорения материальной точки.