Ordm;. Векторный способ задания кругового движения.

Обозначим 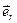орт радиус-вектора точки относительно точки отсчета . Тогда, согласно определению 2, на круговом движении должно выполняться

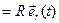, (4)

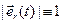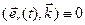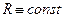, , . (5)

Здесь 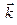— нормаль к плоскости, в которой материальная точка совершает круговое движение. Тождества (5) выполняются при всех значениях из промежутка времени, в течение которого совершается движение.

Орт 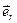меняет свое направление при изменении времени. Задавая такой закон 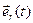изменения направления орта 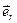, при котором выполняются тождества (5), и подставляя его в (4), придем к векторному способу задания кругового движения точки.

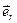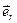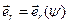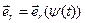В частности, как и при координатном способе (см. п.1º), направление орта можно задавать не непосредственно в зависимости от времени , а, например, через закон изменения угла поворота радиус-вектора точки относительно некоторого фиксированного ее положения. Тогда будет представляться суперпозицией функций и . Так что будем иметь , а задание (4) кругового движения точки примет вид 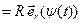, где и 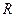удовлетворяют тождествам (5).

Например, если в качестве фиксированного положения точки , от которого отсчитывается угол , взять положение точки 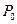(см. рис.6), то при всех на круговом движении точки будет выполняться равенство 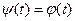, поскольку в таком случае определение угла совпадает с определением угла . Тогда орт 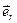и круговое движение точки через закон изменение угла будут задаваться формулами

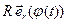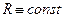, = , . (6)

Легко видеть, что два других тождества (5) для вектор-функции выполняются.

3º. Естественный способ задания кругового движения точки .

В формуле (6) вектор-функция строится через угол , отсчитываемый от положительного направления оси 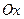в плоскости движения материальной точки. Возможны и другие способы построения этой функции. Например, будем задавать ее через длину дуги окружности.

Будем отсчитывать длину дуги окружности от точки (см. рис.6) пересечения окружности с осью 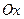. Положительное направление отсчета длины дуги считаем совпадающим с положительным направлением отсчета угла .

Тогда, как известно из геометрии, длина 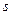дуги 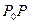выражается через угол соотношением

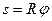. (7)

Подставляя закон движения (2), получаем

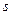= . (8)

Формула (8) дает закон движения точки по окружности в естественной параметризации.

Используя соотношение (7), перейдем в (1) от параметра к длине дуги 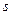. Получим естественную параметризацию траектории движения точки в координатной форме

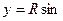
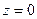, , . (9)

В векторной форме она принимает вид

= , .

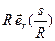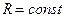Соотношения (9) в совокупности с (8) и (2) дают естественный способ задания кругового движения.