Аналитическая геометрия

Пример 1. Как приложение метода координат для определения местоположения точки, рассмот­рим такой пример.

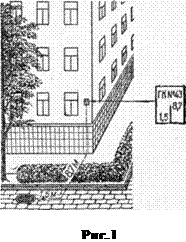Местоположение люка подземного кабеля или водопровода определяют координатами, нанесенными на табличку, укрепленную где-либо на видном месте, считая саму табличку началом координат (рис. 1). Это особенно удобно зимой, когда земля покрыта снегом и найти люк другим путем становится за­труднительно.

Пример 2. На практике часто пользуются понятием уклона, для того чтобы охарактери­зовать положение прямой, т.е. степень ее наклона к горизонтальной плоскости. Так, профиль пути (шоссейного или железнодорожного) можно полностью охарак­теризовать указанием величины k и длиною участка, на котором k практически сохраняет постоянное значение. В пределах каждого такого участка путь считаем прямолинейным.

В качестве примера начертим профиль пути, определенный такими данными:

к=0,12 на участке 0 — 2,0 км »

к=0,2 2,0-- 3,2 км

к=0,05 3,2-5,3-

к=0 5,3 км 7,2 км

к=-0,17 7,2-12,4 –

к=0,16 12,4 км - 15,0 км

Для того чтобы изобразить первый участок, т. е. провести прямую с уклоном откладываем от начала координат по оси х 100 произвольных единиц, в конце этого отрезка восставляем перпендикуляр высотою в 12 таких же единиц и полученную точку соединяем с началом. Другими словами, мы должны построить прямоугольный треугольник с катетами 100 и 12. Тогда его гипотенуза будет иметь уклон k = 0,12 по отношению к катету 100. Остальные участки строим аналогично. Весь профиль пути изображен на рис. 17, причем положитель­ным значениям k соответствуют подъемы, а отрицательным k — спуски. При k = 0 путь идет горизонтально.