Системы уравнений

Пример. На предприятие с работниками четырех категорий привезли заработную плату в купюрах следующего достоинства: по 100 рублей – 1850 купюр, по 50 рублей – 230 купюр, по 10 рублей – 250 купюр, по 1 рублю – 740 купюр. Заработная плата работника первой категории составляет 962 рубля, 2-й категории – 713 руб., 3-й категории – 452 руб., 4-й категории – 261 руб. Определить, сколько сотрудников каждой категории работает на предприятии, если каждому сотруднику выдали заработную плату минимальным числом купюр.

Решение. Условие об оплате минимальным числом купюр является основным в определении количества купюр разного достоинства, выданных сотрудникам разных категорий. Исходя из величины заработной платы по категориям, однозначно определяем таблицу распределения купюр.

Пусть х₁, х₂, х₃, х₄ – количество работников категорий соответственно с первой по четвертую. Тогда по данным таблицы 1 составляем уравнения «баланса», которые образуют систему четырех уравнений с четырьмя неизвестными:

Эту систему можно решить методом Крамера, но удобно решать методом Гаусса, для чего выпишем расширенную матрицу системы, предварительно переместив для удобства первое уравнение на последнее место. Прямой ход метода последовательно меняет вид матрицы:

Таблица 1

Третий переход состоял в перемене мест 3-й и 4-й строк. Полученная в цепочке прямого хода расширенная матрица соответствует системе уравнений, эквивалентной исходной системе:

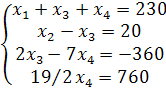
Обратным ходом метода получаем последовательно неизвестные:

x₄ = 80, x₃ = 100, x₂ = 120, x₁ = 50.