
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функция и предел
Задача 1. Разложение некоторого химического вещества протекает в соответствии с уравнением: m(t) = m  е
е  , где m
, где m  — начальное количество вещества, m(t) — количество вещества в момент времени t, к > 0 — некоторая постоянная. Построить график зависимости и проанализировать ее.
— начальное количество вещества, m(t) — количество вещества в момент времени t, к > 0 — некоторая постоянная. Построить график зависимости и проанализировать ее.
Задача 2. С момента начала лечения (вливания глюкозы в кровеносную систему) количество глюкозы в крови m(t) (в мг) изменяется по закону: m(t) = 100 + 50е  , где t — время (в ч). Построить график зависимости и проанализировать ее.
, где t — время (в ч). Построить график зависимости и проанализировать ее.
Задача 3. Размер популяции m(t) животных, начиная с момента времени m  = 0 (время t выражено в годах), изменяется по закону: m(t) = 1500 -
= 0 (время t выражено в годах), изменяется по закону: m(t) = 1500 -  . Что ожидает эту популяцию в будущем?
. Что ожидает эту популяцию в будущем?
Задача 4. В питательную среду вносят популяцию из 1000 бактерий. Численность популяции меняется по закону: Q(t) = 1000 +  где выражается в часах. Описать, что произойдет с популяцией с течением времени.
где выражается в часах. Описать, что произойдет с популяцией с течением времени.
Задача 5. Кривая роста преступности по группе особо опасных преступлений в условных единицах соответствует зависимости по времени у = (140 + a)t - t  , где 3
, где 3  t
t  6, t = 3 соответствует первому году резкого роста, a t = 6 - текущему, и в ближайшие два года прогнозируется та же зависимость по времени. Построить график данной зависимости и ответить на вопрос: когда произойдет перелом в тенденции роста?
6, t = 3 соответствует первому году резкого роста, a t = 6 - текущему, и в ближайшие два года прогнозируется та же зависимость по времени. Построить график данной зависимости и ответить на вопрос: когда произойдет перелом в тенденции роста?
Задача 6. Реакция организма на два лекарства как функции времени (в часах) выражается в виде: r 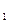 (t) = te
(t) = te  и г
и г  (t) = t
(t) = t 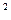 e
e  . Сравните действие этих лекарств на организм.
. Сравните действие этих лекарств на организм.
Задача 7. Имеются данные об изменении во времени коэффициентов рождаемости и смертности (иммиграции и эмиграции). Построить график изменения во времени коэффициента естественного прироста (искусственного прироста, общего прироста).


Время (t) Доза (мг)
Рис. 1. Рис. 2.
Задача 8. На графике изображено положительное и отрицательное воздействие на организм некоторого лекарственного препарата в зависимости от дозы (в млг). Изобразить зависимость общего воздействия на организм данного препарата.
Задача 9. Как, имея графики динамики численности населения региона и доли постоянно проживающего в нем населения, изобразить график динамики численности постоянного населения региона?
Предел
Задача. Численность некоторой популяция х изменяется со временем t, причем эта зависимость задана аналитически. Как спрогнозировать численность популяции в достаточно отдаленном будущем?
Задача 1. Размер популяции m(t) животных, начиная с момента времени t 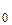 = 0 (время t выражено в годах), изменяется по закону: m(t) = 1500—
= 0 (время t выражено в годах), изменяется по закону: m(t) = 1500—  . Что ожидает эту популяцию в будущем?
. Что ожидает эту популяцию в будущем?
Задача 2. В питательную среду вносят популяцию из 1000 бактерий. Численность популяции меняется по закону: Q(t) = 1000 +  , где t выражается в часах. Описать, что произойдет с популяцией с течением времени.
, где t выражается в часах. Описать, что произойдет с популяцией с течением времени.
Задача 3. Размер популяции животных m(t), начиная с момента времени t 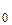 = 0 (в годах), изменяется по закону: m(t) = 1500 -
= 0 (в годах), изменяется по закону: m(t) = 1500 -  . Исследовать функцию m(t), построить ее график и описать, что будет происходить с численностью популяции в дальнейшем.
. Исследовать функцию m(t), построить ее график и описать, что будет происходить с численностью популяции в дальнейшем.
Задача 4. Численность популяций х(t) (функция х(t) соответствует непрерывному росту популяции бактерий от начального размера x(0) до предельного размера) выражается функциями от t:
а) х(t) =100 +  ; б) х(t)=90+10t
; б) х(t)=90+10t  ; в) х(t) = 10 + 100е
; в) х(t) = 10 + 100е  ;
;
г) х(t) = 10е  ; д(t) = 10е
; д(t) = 10е  .
.
В каждом случае найти предельные размеры популяций и начальную популяцию x(0).
Задача 5. Популяция бактерий увеличивается от начального размера
до размера p(t) в момент t (дни) согласно уравнению p(t) =  .
.
Найдите  p(t) — равновесную популяцию.
p(t) — равновесную популяцию.
Задача 6. При вливании глюкозы ее содержание в крови больного
спустя t  составляет c(t)= 10 — 8е
составляет c(t)= 10 — 8е  . Найдите
. Найдите  с(t) = 0 - равновесное состояние содержания глюкозы в крови.
с(t) = 0 - равновесное состояние содержания глюкозы в крови.
Задача 7. С момента начала лечения (вливания глюкозы в кровеносную систему) количество глюкозы в крови m(t) (в мг) изменяется по закону: m(t) = 100 + 50е  , где t — время (в ч). Построить график зависимости и проанализировать ее.
, где t — время (в ч). Построить график зависимости и проанализировать ее.
Задача 8. Пусть функция у = f(t) отражает зависимость числа жителей поселка у от временного показателя t. Объясните смысл записи  f(t) = 0.
f(t) = 0.
Задача 9. Ток в электрической цепи изменяется в зависимости от времени по закону I(t) =  .
.
Найти величину тока в переходном процессе (в момент включения / выключения), то есть при t  0.
0.
Задача 10. Падение напряжения на концах некоторого внешнего сопротивления R, подключенного к источнику Э.Д.С., согласно закону Ома, равно
U =  ,
,
где r – внутреннее сопротивление источника Э.Д.С.; Е – величина Э.Д.С. источника тока.
 Рассмотреть выражение закона Ома как функцию f (R), найти её предел при R
Рассмотреть выражение закона Ома как функцию f (R), найти её предел при R  и сделать вывод.
и сделать вывод.
Задача 11.Катет а прямоугольного треугольника разделен на n равных частей, и на получившихся отрезках построены вписанные прямоугольники (рис. 1). Определить предел площади образовавшейся ступенчатой фигуры, если n  .
.
Задача 12. Некоторый химический процесс протекает так, что прирост количества вещества за каждый промежуток времени  из бесконечной последовательности промежутков (i
из бесконечной последовательности промежутков (i  , (i+1)
, (i+1)  ) (i = 0, 1,2, ...) пропорционален наличному количеству вещества, имеющемуся в начале этого промежутка, и величине промежутка. Предполагая, что в начальный момент времени количество вещества составляло Q
) (i = 0, 1,2, ...) пропорционален наличному количеству вещества, имеющемуся в начале этого промежутка, и величине промежутка. Предполагая, что в начальный момент времени количество вещества составляло Q 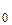 , определить количество вещества Q
, определить количество вещества Q  через промежуток времени t, если прирост количества вещества происходит каждую n-ю часть промежутка времени
через промежуток времени t, если прирост количества вещества происходит каждую n-ю часть промежутка времени  = t/n.
= t/n.
Найти Q  =
= 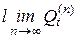 .
.
Задача 13. Круглая пластина радиусом а с закрепленными краями находится под действием силы Р, приложенной к ее центру. Прогиб на расстоянии х от центра пластины выражается следующей формулой:
y = Pkx 
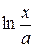 + P
+ P  (a
(a  - x
- x  )
)
где k — коэффициент, связанный с прочностными характеристиками материала и формой пластины. Найти прогиб в центре пластины.
Задача 14. Шарнирно-опорная балка под действием равномерно распределенной нагрузки q и сжимающей силы N прогибается. Прогиб в середине балки вычисляется по формуле
f = 
где u =  ; EI — жесткость балки;
; EI — жесткость балки;  — длина балки.
— длина балки.
Показать, что: а) при u  0 (El
0 (El  ) балка не должна прогибаться, т. е. f
) балка не должна прогибаться, т. е. f  0; б) при u
0; б) при u 
 (N
(N 
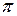
 ЕI /
ЕI / 
 ) f
) f  , т. е. существует критическая сила, при которой балка «разрушается», что математически соответствует ее бесконечному прогибу.
, т. е. существует критическая сила, при которой балка «разрушается», что математически соответствует ее бесконечному прогибу.
Задача 15. Динамическая самоиндукция антенны при удлинении волны выражается формулой L = L 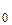
 ,
,
где L — динамическая самоиндукция; L 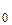 — статическая самоиндукция;
— статическая самоиндукция;  — действующая длина антенны;
— действующая длина антенны;  — длина волны антенны. Найти
— длина волны антенны. Найти 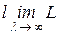 .
.
Задача 16. В теории ламповых генераторов доказывается, что коэффициент полезного действия генератора 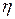 выражается через угол
выражается через угол 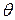 отсечки тока формулой
отсечки тока формулой 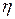 =
=  , где
, где  — коэффициент использования напряжений. Найти
— коэффициент использования напряжений. Найти  .
.
Задача 17. Расчет рабочих колес турбины приводит к уравнению
 n у = —k
n у = —k  x
x  +
+  n уа,
n уа,
где у — толщина колеса на расстоянии х от оси вращения; у = у  при х = 0.
при х = 0.
Найти 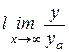 .
.
Задача 18. В атомной физике изучается формула Релея —Джинса, дающая зависимость распределения энергии излучения от частоты: u  = А —
= А —  . Считая
. Считая  малой величиной, упростить формулу способом линеаризации, считая d
малой величиной, упростить формулу способом линеаризации, считая d  постоянной величиной.
постоянной величиной.
Решение. Если v мало, то  = 1, т.е.
= 1, т.е. 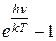 ~
~ 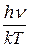 или
или 
 1 +
1 + 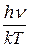 , тогда u
, тогда u 
 A
A 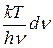 .
.
Задача 19. Имеется с 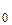 грамм-молекул активного вещества. Предполагая, что в единицу времени вступает в реакцию р% этого вещества, узнать, какое количество грамм-молекул не вступит в реакцию по истечении времени t.
грамм-молекул активного вещества. Предполагая, что в единицу времени вступает в реакцию р% этого вещества, узнать, какое количество грамм-молекул не вступит в реакцию по истечении времени t.
Решение. Через единицу времени вступают в реакцию 0,01рс 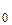 грамм-молекул; остаются с
грамм-молекул; остаются с 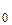 (1 —
(1 —  ). Через 2 единицы времени не вступило в реакцию с
). Через 2 единицы времени не вступило в реакцию с 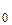 (1 —
(1 —  )
)  . Через t единиц времени количество грамм-молекул с
. Через t единиц времени количество грамм-молекул с 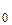 (1 —
(1 —  )
)  . Для лучшего приближения к действительности единицу времени разобьем на n более мелких частей. Тогда вещества, не вступившего в реакцию, будет с
. Для лучшего приближения к действительности единицу времени разобьем на n более мелких частей. Тогда вещества, не вступившего в реакцию, будет с 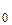 (1 —
(1 —  )
)  , или, полагая
, или, полагая  = k, получим (1 – k)
= k, получим (1 – k) 
 1 - kt
1 - kt  = 1 – kt/n, тогда вещества, не вступившего в реакцию, будет
= 1 – kt/n, тогда вещества, не вступившего в реакцию, будет
с 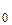 (1 — kt/n)
(1 — kt/n)  .
.
Истинное количество остающегося вещества
с =  = c
= c 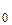 e
e  .
.
Задача 20. Упростить барометрическую формулу
h = 800 (1 + 0,004t)  n
n  , принимая
, принимая  =
=  ,
,
где 0  x
x  1.
1.
Ответ. h =  .
.
Задача 21. В топографии возникает необходимость найти отношение стрелы f = DB (высоты сегмента) дуги ABC окружности радиуса r к стреле f  = D
= D  B
B  половины АВ
половины АВ  В этой дуги, если центральный угол АОВ мал. Найти это отношение.
В этой дуги, если центральный угол АОВ мал. Найти это отношение.
Указание. Построить центральные углы дуг и использовать принцип эквивалентности бесконечно малых.
Ответ.  4.
4.
Задача 22. «В педагогическом эксперименте сравниваются результаты по двум различным методикам обучения. Материал темы излагается в двух группах, где применялись единые тестовые задания. В качестве переменной выступает безразмерная величина х = t/Т (0 <t < Т), где T - общее количество часов для изучения темы.
Средние коэффициенты усвоения темы, в зависимости от степени «погружения» в теоретический материал, для каждой группы выражаются функциями 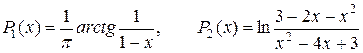 .
.
Как выяснить эффективность предложенных методик?»
Этап анализа позволяет сделать вывод о том, что для данных зависимостей требуется сравнить значения Р  (1) и Р
(1) и Р  (1), которые непосредственно из формул определить нельзя.
(1), которые непосредственно из формул определить нельзя.
На этапе классификации выясняется, что каждая функция является комбинацией конечного числа элементарных, поэтому для 0 < х < 1 функции непрерывные.
Этап расчленения целого на части дает возможность выявить, что для установления результата к концу обучения следует найти пределы указанных функций при х  1, сравнив значения между собой. Надо сказать, что понятие предела, сложное по своей природе, приобретает здесь вполне конкретные очертания.
1, сравнив значения между собой. Надо сказать, что понятие предела, сложное по своей природе, приобретает здесь вполне конкретные очертания.
На этапе установления и определения последовательностей возникает проблема вычисления предела сложной функции. В первом случае аргумент является бесконечно большой величиной, а во втором — представляет собой «неопределенность вида 0/0 «.
Использование теоремы о предельном переходе под знаком непрерывной функции завершается на этапе определения взаимосвязей.
На этапе синтеза сравниваются два предельных значения Р  (1) = 1/2, Р
(1) = 1/2, Р  (1) = Ln 2 и делаются выводы.
(1) = Ln 2 и делаются выводы.
Задача 23. Задача предложена в учебнике Б.В.Гнеденко и отмечено, что ее сюжет заимствован из звездной астрономии. "В сфере радиуса R случайно и независимо друг от друга разбросано n точек. Чему равна вероятность того, что расстояние от центра сферы до ближайшей точки будет не менее r, если r < R?" Решая эту задачу, студенты получают ответ р = 1-(1 -  )
)  . Можно предложить выяснить, к чему будет стремиться полученная вероятность (и объяснить полученный ответ) при следующих условиях:
. Можно предложить выяснить, к чему будет стремиться полученная вероятность (и объяснить полученный ответ) при следующих условиях:
1) n, r фиксированы, R  ;
;
2) n, R фиксированы, r  R;
R;
3) n, R фиксированы, r  0;
0;
4) n, R фиксированы, r  ;
;
5) n, R  , причем
, причем  .
.
( в звездной астрономии в окрестности Солнца  0,0063, если R измерено в парсеках).
0,0063, если R измерено в парсеках).
24.В расчетной практике по абсорбции, дистилляции, экстракции и выщелачиванию встречается функция f(х) =  .
.
Найти предел этой функции при х 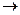 1.
1.
25. В начальный момент времени радиоактивный образец содержит N 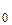 ядер. Распад происходит таким образом, что быстрота уменьшения числа нераспавшихся ядер в любой момент времени пропорциональна наличному количеству нераспавшихся ядер к началу указанного момента времени (коэффициент пропорциональности
ядер. Распад происходит таким образом, что быстрота уменьшения числа нераспавшихся ядер в любой момент времени пропорциональна наличному количеству нераспавшихся ядер к началу указанного момента времени (коэффициент пропорциональности  ). Найти закон изменения числа нераспавшихся ядер со временем.
). Найти закон изменения числа нераспавшихся ядер со временем.
26. Скорость вывода массы лекарственного препарата из крови при однократном его введении со временем пропорциональна массе препарата в данный момент времени. Найти закон изменения массы препарата в крови со временем, если m(0)= m 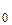 , к - коэффициент пропорциональности.
, к - коэффициент пропорциональности.
27. Конденсатор емкостью С замкнут на сопротивление R. Первоначальный заряд конденсатора известен и равен q 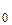 . Найти закон изменения заряда со временем q(t).
. Найти закон изменения заряда со временем q(t).
28. Пучок света интенсивностью I 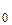 падает на поверхность вещества. Найти закон изменения интенсивности от расстояния, пройденного светом в веществе, полагая, что быстрота уменьшения интенсивности в некоторой точке с увеличением расстояния пропорциональна величине интенсивности (коэффициент пропорциональности
падает на поверхность вещества. Найти закон изменения интенсивности от расстояния, пройденного светом в веществе, полагая, что быстрота уменьшения интенсивности в некоторой точке с увеличением расстояния пропорциональна величине интенсивности (коэффициент пропорциональности  ).
).
29. Лодка массой m двигалась в воде с постоянной скоростью v 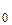 . В некоторый момент времени двигатель выключается. Найти закон дальнейшего изменения скорости со временем, считая силу сопротивления пропорциональной скорости (коэффициент пропорциональности к).
. В некоторый момент времени двигатель выключается. Найти закон дальнейшего изменения скорости со временем, считая силу сопротивления пропорциональной скорости (коэффициент пропорциональности к).
30.Первоначальный вклад в банк составил S(0) = 1000 усл. единиц. Найти наращенное за 10 лет значение суммы, если оно реинвестируется по постоянной ставке i  = 25 % при следующих значениях m: а) 1 раз в год; б) ежеквартально; в) непрерывно.
= 25 % при следующих значениях m: а) 1 раз в год; б) ежеквартально; в) непрерывно.
31.Количество возможных клиентов некоторой фирмы, в результате хорошо организованной рекламы, увеличивается со временем пропорционально количеству знающих об услугах этой фирмы в данный момент. Найти закон изменения количества клиентов, если М(0)= А 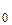 , с - коэффициент пропорциональности. Как изменится количество клиентов через два дня, если за первый день количество возможных клиентов возросло на 25%.
, с - коэффициент пропорциональности. Как изменится количество клиентов через два дня, если за первый день количество возможных клиентов возросло на 25%.
32.Лодка массой m двигалась в воде с постоянной скоростью v  . В некоторый момент времени двигатель выключается. Найти закон дальнейшего изменения скорости со временем, считая силу сопротивления пропорциональной скорости (коэффициент пропорциональности к).
. В некоторый момент времени двигатель выключается. Найти закон дальнейшего изменения скорости со временем, считая силу сопротивления пропорциональной скорости (коэффициент пропорциональности к).
33. Скорость вывода массы лекарственного препарата из крови при однократном его введении со временем пропорциональна массе препарата в данный момент времени. Найти закон изменения массы препарата в крови со временем, если m(0) = m  , где к – коэффициент пропорциональности.
, где к – коэффициент пропорциональности.
Литература по прикладные задачи
1. Беляев. Сборник задач по сопротивлению материалов. М.: Наука, 1972. 832 с.
2. Запорожец Г.И. Руководство к решению задач по математическому анализу. М.: Высшая школа, 1966. 460 с.
3. Зельдович Я.Б., Мышкис А.Д. Элементы прикладной математики. М.: Наука, 1972. 462 с.
4. Зельдович Я.Б., Яглом И.М. Высшая математика для начинающих физиков и техников. М.: Наука, 1982. 512 с.
5. Зетель С.И. Задачи на максимум и минимум. М.; Л.: Гостехиздат 1948. 224 с.
6. Минорский В.П. Сборник задач по высшей математике. М.: Госиздат, 1968. 359 с.
7. Ноздрин И.Н., Степаненко И.М., Костюк Л.К. Прикладные задач по высшей математике. Киев, Вища школа, 1976, 176 с.
8.Очан Ю.С. Методы математической физики. М.: Высшая школа, 1965. 320 с.
9.Пономарев К.К. Составление и решение дифференциальных уравнений инженерно-технических задач. М.: Учпедгиз, 1948. 98 с
10.Соболев С.Л. Уравнения математической Физики. М.-Л.: ОГИЗ, 1947. 248 с.
Дата добавления: 2015-04-15; просмотров: 401; Мы поможем в написании вашей работы!; Нарушение авторских прав |