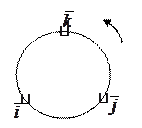КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Векторное произведение двух векторов
1. Определение. Векторным произведением двух векторов называется вектор, удовлетворяющий трём условиям:

| 1)  ; 2) ; 2) 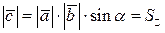 ;
3) векторы ;
3) векторы 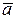 , , 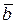 , ,  образуют правую тройку векторов (из конца вектора образуют правую тройку векторов (из конца вектора  кратчайший поворот от кратчайший поворот от 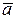 к к 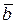 виден против часовой стрелки). Записывается виден против часовой стрелки). Записывается  или или  . .
|
Свойства векторного произведения
10.  антикоммутативность. антикоммутативность.
| |||||||||||||||||||||
20.  дистрибутивность относительно числового
множителя. дистрибутивность относительно числового
множителя.
| |||||||||||||||||||||
30.  дистрибутивность относительно сложения. дистрибутивность относительно сложения.
| |||||||||||||||||||||
40.  тогда и только тогда, когда тогда и только тогда, когда  , или , или  , или , или  .
В частности, .
В частности,  . .
| |||||||||||||||||||||
50Теорема 4.Если векторы 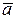 и и 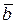 в ДСК заданы своими координатами в ДСК заданы своими координатами   и и 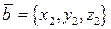 , то , то  .
Доказательство.Разложим векторы .
Доказательство.Разложим векторы 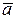 и и 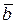 по базису по базису 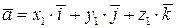 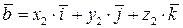 . Заполним таблицу. . Заполним таблицу.
| |||||||||||||||||||||
|
|
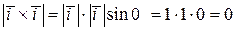 , ,
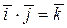 , , 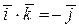 и т.д. и т.д.
| |||||||||||||||||||
    
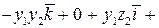  
  , ч.т.д. , ч.т.д.
|
3. Геометрический смысл векторного произведения.
 ;
; 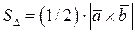 .
.
Замечание: Векторное произведение может быть выражено формулой: 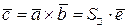 , где
, где 
 орт направления вектора
орт направления вектора  .
.
Дата добавления: 2014-11-13; просмотров: 254; Мы поможем в написании вашей работы!; Нарушение авторских прав |