
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства скалярного произведения.
10.   коммутативность сложения (переместительный закон). коммутативность сложения (переместительный закон).
| |||
20.   дистрибутивность (распределительный закон относительно сложения). дистрибутивность (распределительный закон относительно сложения).
| |||
30.   ассоциативность (сочетательный закон относительно умножения на число ассоциативность (сочетательный закон относительно умножения на число  ). ).
| |||
40.  . .
| |||
| В векторной форме | В ДОСК | ||
50.  . .
| 50.  . .
| ||
60.  . .
| 60.  . .
| ||
70.   условие ортогональности.
условие ортогональности.
| 70.  , ,
 , ,  . .
| ||
|
80.
| 80.  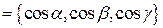 , ,
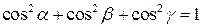 . .
| ||
 90. 90.
| 90.
 . .
| ||
Докажем сойство 7.Теорема 3.Скалярное произведение векторов равно нулю тогда и только тогда, когда эти векторы ортогональны т.е.  . .
| |||
1) Необходимое условие.
Дано:  .
Доказать: .
Доказать:  .
Доказательство.Так как по условию .
Доказательство.Так как по условию
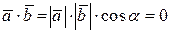 , т.к. , т.к.  по условию, то по условию, то  ,
Следовательно, угол ,
Следовательно, угол  и и  . .
| 2) Достаточное условие.
Дано:  .
Доказать: .
Доказать:  Доказательство.Так как по условию
Доказательство.Так как по условию  , значит угол , значит угол  , тогда , тогда 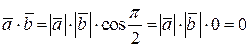 , ч.т.д. , ч.т.д.
| ||
2. Физический смысл скалярного произведения.
Пусть материальная точка движется прямолинейно от точки  к точке к точке 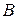
| ||
под действием постоянной силы  , направленной под углом , направленной под углом  к направлению к направлению
| ||
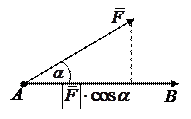
| движения. Тогда работа, совершаемая при этом движении, равна:
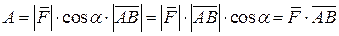 , т.е. , т.е.  . .
|
Дата добавления: 2014-11-13; просмотров: 273; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 .
.