
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейные операции над векторами. Задача 1. В равнобедренной трапеции ABCD угол АDС равен , , и
Задача 1. В равнобедренной трапеции ABCD угол АDС равен  ,
, 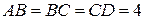 ,
, 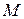 и
и 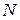
 середины сторон
середины сторон 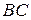 и
и 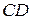 соответственно. Выразить векторы
соответственно. Выразить векторы  через
через 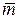 и
и 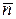
 орты направлений
орты направлений 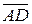 и
и  .
.
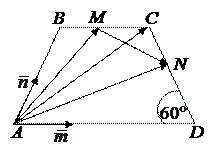 Решение.
Решение.
Выберем треугольник, в который входит
неизвестный вектор, а два других либо даны, либо их можно найти.
4) Из 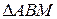 имеем: имеем: 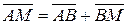 . Так как . Так как 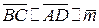 и и 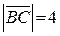 , то , то 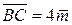 , ,  . .
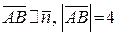 , то , то  . Тогда . Тогда 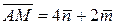
|
5) Из  имеем:
имеем: 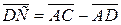 ;
;  .
.
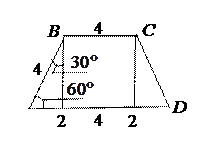
| Для нахождения вектора 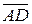 определим его длину.
Из условия определим его длину.
Из условия 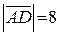 , следовательно , следовательно  .
Тогда .
Тогда 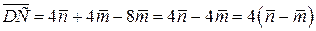 ,
т.е. ,
т.е. 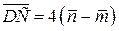 . .
|
6) Из  :
: 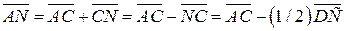 .
.
 ,
, 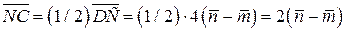 .
.
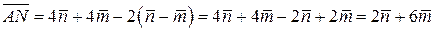 , т.е.
, т.е. 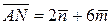 .
.
7) Из 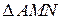 :
: 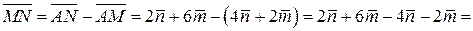
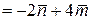 ,
, 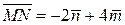 .
.
Задача 2.Найти орт биссектрисы угла между двумя векторами 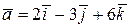 и
и  .
.
Решение. Перенесём векторы 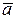 и
и 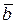 в одну точку. Диагональ четырёхугольника
в одну точку. Диагональ четырёхугольника
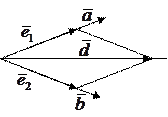
| совпадает с биссектрисой угла, если четырёхугольник ромб. Если найти орты направлений, то получим векторы 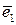 и и   единичной длины. Построим на единичной длины. Построим на 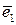 и и  параллелограмм, который будет являться ромбом. параллелограмм, который будет являться ромбом.
|
Следовательно, диагональ делит угол ромба пополам, т.е. является биссектрисой угла. Найдём 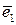 и
и  . Векторы
. Векторы 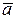 и
и 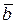 имеют координаты:
имеют координаты: 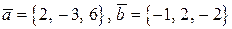 , тогда
, тогда 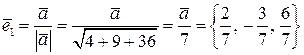 ,
, 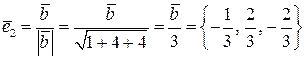 ,
, 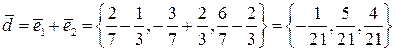 ,
,
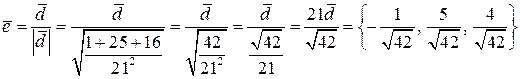 .
.
Задача 3.Образуют ли векторы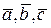 базис в пространстве
базис в пространстве 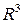 ? Если да, то найти линейную зависимость вектора
? Если да, то найти линейную зависимость вектора 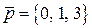 от векторов
от векторов  ,
, 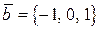 и
и 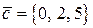 .
.
Решение. Три вектора  образуют базис в
образуют базис в 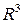 тогда и только тогда, когда они линейно независимы. Аналитически это означает, что уравнение
тогда и только тогда, когда они линейно независимы. Аналитически это означает, что уравнение 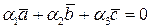 с неизвестными
с неизвестными 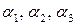 имеет единственное нулевое решение, а это означает, что определитель системы
имеет единственное нулевое решение, а это означает, что определитель системы 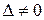 . Составим систему:
. Составим систему:
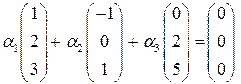 , т.е.
, т.е. 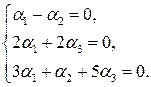



 ,
,
следовательно, система имеет единственное решение 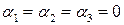 , тогда,
, тогда,
векторы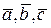 линейно независимы и образуют базис. Поэтому, вектор
линейно независимы и образуют базис. Поэтому, вектор  можно разложить по данному базису единственным образом, т.е.
можно разложить по данному базису единственным образом, т.е. 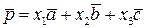 :
:
 . Решим систему
. Решим систему  методом Гаусса.
методом Гаусса.

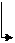




 .
.
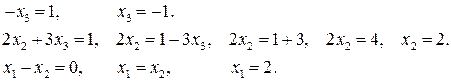
Получим  .
.
Дата добавления: 2014-11-13; просмотров: 419; Мы поможем в написании вашей работы!; Нарушение авторских прав |