
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
Модуль вектора через координаты
Пусть вектор 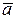 задан своими координатами задан своими координатами  . .
|   
| Тогда вектор 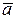 является диагональю является диагональю  прямоугольного параллелепипеда с длинами сторон прямоугольного параллелепипеда с длинами сторон  . Применяя дважды теорему
Пифагора, получим: . Применяя дважды теорему
Пифагора, получим:  , , 
| 2.9. Расстояное между двумя точками

| Пусть заданы точки  и и  .
Вектор .
Вектор  , следовательно, , следовательно, 
 . .
|
Деление отрезка в данном отношении
Пусть на прямой  задан отрезок АВ, где задан отрезок АВ, где  , ,  , и точка , и точка  , лежащая внутри отрезка АВ. Тогда, если , лежащая внутри отрезка АВ. Тогда, если   , то говорят, что точка , то говорят, что точка  делит отрезок АВ в отношении делит отрезок АВ в отношении  внутренним образом. Следовательно, внутренним образом. Следовательно,  и и  . Отсюда имеем . Отсюда имеем
 , ,  , ,  , ,
| | |   Аналогично получаем: Аналогично получаем:
 Если
Если 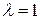 , то точка , то точка   середина отрезка середина отрезка  ,
тогда координаты середины отрезка вычисляются по формулам: ,
тогда координаты середины отрезка вычисляются по формулам:
|    Если
Если  , то точка , то точка  совпадет с точкой A. Если точка совпадет с точкой A. Если точка  не лежит внутри отрезка не лежит внутри отрезка  , то , то  . В этом случае векторы . В этом случае векторы    , следовательно, , следовательно,  , векторы сонаправлены , векторы сонаправлены    и = и =  . .
|
|

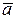 задан своими координатами
задан своими координатами  .
.



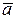 является диагональю
является диагональю  прямоугольного параллелепипеда с длинами сторон
прямоугольного параллелепипеда с длинами сторон  . Применяя дважды теорему
Пифагора, получим:
. Применяя дважды теорему
Пифагора, получим:  ,
, 

 и
и  .
Вектор
.
Вектор  , следовательно,
, следовательно, 
 .
.

 Аналогично получаем:
Аналогично получаем:
 Если
Если 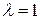 , то точка
, то точка 
 середина отрезка
середина отрезка  ,
тогда координаты середины отрезка вычисляются по формулам:
,
тогда координаты середины отрезка вычисляются по формулам:


 Если
Если  , то точка
, то точка  совпадет с точкой A. Если точка
совпадет с точкой A. Если точка  не лежит внутри отрезка
не лежит внутри отрезка  , то
, то  . В этом случае векторы
. В этом случае векторы 

 , следовательно,
, следовательно,  , векторы сонаправлены
, векторы сонаправлены 

 и =
и =  .
.

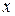

 задан отрезок АВ, где
задан отрезок АВ, где  ,
,  , и точка
, и точка  , лежащая внутри отрезка АВ. Тогда, если
, лежащая внутри отрезка АВ. Тогда, если 
 , то говорят, что точка
, то говорят, что точка  внутренним образом. Следовательно,
внутренним образом. Следовательно,  и
и  . Отсюда имеем
. Отсюда имеем
 ,
,  ,
,  ,
,