
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейная зависимость между векторами
Определение.Результат конечного числа линейных операций  называется линейной комбинацией векторов
называется линейной комбинацией векторов  .Числа
.Числа  называются коэффициентамилинейной комбинации. В равенстве
называются коэффициентамилинейной комбинации. В равенстве  вектор
вектор  является линейной комбинацией векторов
является линейной комбинацией векторов  или вектор
или вектор  линейно выражается через векторы
линейно выражается через векторы  .
.
Например, вектор  является линейной комбинацией векторов
является линейной комбинацией векторов  с коэффициентами 3, 4,
с коэффициентами 3, 4,  7 соответственно.
7 соответственно.
Определение.Векторы  называются линейно зависимыми, если существуют числа
называются линейно зависимыми, если существуют числа  , среди которых хотя бы одно число отлично от нуля, и такие, что выполняется:
, среди которых хотя бы одно число отлично от нуля, и такие, что выполняется:  .
.
Определение.Векторы  называются линейно независимыми, если равенство
называются линейно независимыми, если равенство  выполняется только при
выполняется только при .
.
Замечания:
1) если хотя бы один из векторов нулевой, то векторы линейно зависимы;
2) если хотя бы один из векторов является линейной комбинацией остальных векторов, то векторы линейно зависимы;
3) два вектора линейно зависимы  когда они коллинеарны;
когда они коллинеарны;
4) три вектора линейно зависимы  когда они компланарны.
когда они компланарны.
Определение. Базисом линейного пространства называется упорядоченная система векторов  этого пространства, которая удовлетворяет двум условиям:
этого пространства, которая удовлетворяет двум условиям:
а) векторы системы  линейно независимы;
линейно независимы;
б) всякий вектор пространства является линейной комбинацией векторов системы  .
.
Число векторов базиса называется размерностью пространства. Пространство, в котором базис состоит из  векторов
векторов  , называется
, называется  мерным,обозначается
мерным,обозначается  . Векторы
. Векторы  называются базисными. Любые n линейно независимых векторов этого пространства образуют его базис. Если задан базис, то каждый вектор
называются базисными. Любые n линейно независимых векторов этого пространства образуют его базис. Если задан базис, то каждый вектор  имеет единственное разложение по этому базису.
имеет единственное разложение по этому базису.
Определение.Пусть n=3, тогда 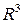
 трехмерное векторное пространство. Базисом в пространстве
трехмерное векторное пространство. Базисом в пространстве 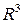 называется любая упорядоченная тройка некопланарных векторов
называется любая упорядоченная тройка некопланарных векторов  . Любой вектор
. Любой вектор  этого пространства можно разложить по данному базису единственным образом, т.е.
этого пространства можно разложить по данному базису единственным образом, т.е.  .
.
Определение.Если n=2, то  двумерное пространство (плоскость). Базисом на плоскости называеся любая упорядоченная пара неколлинеарных векторов
двумерное пространство (плоскость). Базисом на плоскости называеся любая упорядоченная пара неколлинеарных векторов  и любой вектор этого пространства можно разложить по данному базису единственным образом, т.е.
и любой вектор этого пространства можно разложить по данному базису единственным образом, т.е.  .
.
Определение.Базисом на прямой называется любой ненулевой вектор этой прямой. Пусть базис состоит из одного вектора  Тогда любой вектор этой прямой будет коллинеарен вектору,
Тогда любой вектор этой прямой будет коллинеарен вектору, 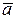 а это означает, что будет выполняться равенство
а это означает, что будет выполняться равенство  . Это равенство означает разложение вектора
. Это равенство означает разложение вектора  по данному базису.
по данному базису.
Замечание.
 если три вектора если три вектора  , , 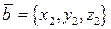 и и   линейно зависимы, например, линейно зависимы, например,  . Это означает, что в определителе . Это означает, что в определителе
 строки линейно зависимы, значит, определитель строки линейно зависимы, значит, определитель  ; ;
 если если 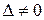 , то векторы , то векторы  , , 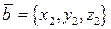 и и  линейно независимы и образуют базисв трехмерном пространстве.В этом случае любой четвертый вектор трехмерного пространства является линейной комбинацией базисных векторов: линейно независимы и образуют базисв трехмерном пространстве.В этом случае любой четвертый вектор трехмерного пространства является линейной комбинацией базисных векторов: 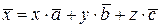 , где , где  координаты вектора координаты вектора  в базисе в базисе  ; ;
|
Дата добавления: 2014-11-13; просмотров: 300; Мы поможем в написании вашей работы!; Нарушение авторских прав |