
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейные операции над геометрическими векторами
1. Аветисов Э.С., Аветисов С.Э., Белоглазов В.Г. и др. Глазные болезни: Учебник.– М.: Медицина, 2002.– 559 с.
2. Вит В.В. Строение зрительной системы человека: учебное пособие.– Одесса: Астропринт, 2003.– 655 с.
3. Даниличев В.Ф. Современная офтальмология.– Спб: «Питер», 2000.– 666 с.
4. Должич Г.И. Глазные болезни в вопросах и ответах.– Ростов-на-Дону: «Феникс», 2000.– 413 с.
5. Жабоєдов Г.Д., Сергієнко М.М. Очні хвороби.– Київ: «Здоров’я», 1999.– 309 с.
6. Морозов В.И., Яковлев А.А. Фармакотерапия глазных болезней: Справочник.– М.: Медицина, 2001.– 461 с.
7. Кански Д. Клиническая офтальмология: систематизированный подход. Перевод с английского.– М.: Логосфера, 2006.– 733 с.
8. Мальцев Э.В., Павлюченко К.П. Биологические особенности и заболевания хрусталика.– Одесса: Астропринт, 2002– 445 с.
9. Павлюченко К.П., Олейник Т.В., Могілевський С.Ю. та. ін. Очні хвороби: навчально-методичний посібник.– Донецьк, Апекс, 2004.– 112 с.
СВЕДЕНИЯ ОБ АВТОРАХ:
Сотрудники кафедры глазных болезней ДонНМУ им. М.Горького:
Павлюченко Константин Павлович, доктор медицинских наук, профессор, заведующий кафедры глазных болезней ДонНМУ;
Олейник Татьяна Викторовна, кандидат мед. наук, доцент кафедры глазных болезней;
Зыков Игорь Геронтьевич, кандидат мед. наук, доцент кафедры глазных болезней;
Могилевский Сергей Юрьевич, доктор мед. наук, профессор кафедры глазных болезней;
Белоусова Зоя Филипповна, кандидат мед. наук, доцент кафедры глазных болезней;
Гавриленко Ирина Николаевна, кандидат мед. наук, доцент кафедры глазных болезней;
Иващенко Сергей Евгеньевич, кандидат мед. наук, доцент кафедры глазных болезней;
Черняева Светлана Николаевна, кандидат мед. наук, ассистент кафедры глазных болезней.
ВЕКТОРЫ И ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД НИМИ
Основные понятия
1. Величины бывают скалярными и векторными. Скалярные величины определяются своими численными значениями, например, масса, время, длина, площадь, объём и др. Такие величины как ускорение, сила, момент силы и др. имеют две характеристики численное значение и направлениеи называютсявекторнымииливекторами.Для обозначения вектора используют отрезок, на котором указано направление, т.е. направленный отрезок, его обозначают 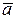 или
или  , где точка
, где точка  есть начало вектора
есть начало вектора 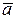 , точка
, точка 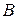
 конец вектора
конец вектора 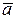 (рис.1). Начало вектора будем называть точкой приложения.
(рис.1). Начало вектора будем называть точкой приложения.
|
 Определение.Вектор, длина которого равна единице, называется единичным вектором или ортом направления. Обозначается Определение.Вектор, длина которого равна единице, называется единичным вектором или ортом направления. Обозначается  .
Вектор .
Вектор  имеет длину, равную единице имеет длину, равную единице  ,
и сохраняет направление вектора ,
и сохраняет направление вектора  .
Орты на плоскости изображены на рис.2 .
Орты на плоскости изображены на рис.2
|
3. Определение.Два вектора называются равными, если они имеют
одинаковую длину и одинаковое направление. На рис.3 изображён ромб
со стороной, равной 1. Тогда  , но
, но 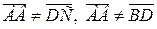 .
.
 
| Векторы  и и  называются противоположными. называются противоположными.  Сумма противоположных векторов равна нулю, т.е. Сумма противоположных векторов равна нулю, т.е.  .
Замечание: .
Замечание:  или или  . .
|
4. Определение.Два вектора или более, лежащие на параллельных
прямых или на одной прямой, называются коллинеарными. Обозначается  . На рис.3
. На рис.3  или
или 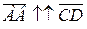 ,
,  ,
, 

 и т. д.
и т. д.
Определение.Так как направление нулевого вектора не определено, то он коллинеарен любому вектору.
Определение.Два вектора называются ортогональными, если они лежат на взаимно перпендикулярных прямых. Обозначается  .
.
Определение.Три или более векторов, лежащих в параллельных плоскостях (или в одной плоскости), называются компланарными. На рис.3 все векторы компланарны. Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над геометрическими векторами
Линейными операциями над векторами называют операцию сложения векторов и операцию умножения вектора на скаляр (число).
| 1. Сложение векторов. |
 а) Правило треугольника: а) Правило треугольника: 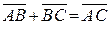 . Суммой векторов . Суммой векторов  и и  называется вектор называется вектор 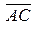 , идущий из начала первого вектора в конец второго или , идущий из начала первого вектора в конец второго или  . .
|
 б) Правило многоугольника б) Правило многоугольника  или или
 . .
| ||||
 в) Если векторы образуют замкнутый многоугольник, как показано на рисунке, то сумма векторов равна нулю: в) Если векторы образуют замкнутый многоугольник, как показано на рисунке, то сумма векторов равна нулю:

| ||||
г) Правило параллелограмма:  . Под суммой двух векторов . Под суммой двух векторов
| ||||

| с общим началом понимается вектор  , выходящий из общего начала и совпадающий по длине и направлению с диагональю параллелограмма, построенного на этих векторах. , выходящий из общего начала и совпадающий по длине и направлению с диагональю параллелограмма, построенного на этих векторах.
| |||
 2. Вычитание векторов. 2. Вычитание векторов.
| ||||
«уменьшаемого» (вторая диагональ параллелограмма), Выражение | ||||
| 3. Умножение вектора на число. | ||||

| При умножении вектора на число  длина вектора умножается на это число, а направление не изменяется. При умножении вектора на число длина вектора умножается на это число, а направление не изменяется. При умножении вектора на число  длина умножается на число длина умножается на число  , а направление изменяется на противоположное. , а направление изменяется на противоположное.
| |||
Дата добавления: 2014-11-13; просмотров: 307; Мы поможем в написании вашей работы!; Нарушение авторских прав |

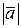 или
или  . Вектор, длина которого равна нулю,
называется нулевым вектором и обозначается
. Вектор, длина которого равна нулю,
называется нулевым вектором и обозначается 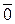 или просто 0.
или просто 0.
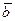 понимается вектор
понимается вектор  , который в сумме
с вектором
, который в сумме
с вектором 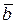 дает вектор
дает вектор  .
Другими словами, это вектор, идущий из
конца «вычитаемого» вектора в конец
.
Другими словами, это вектор, идущий из
конца «вычитаемого» вектора в конец
 .
. можно записать иначе
можно записать иначе  . Эту формулу читают так: чтобы из вектора
. Эту формулу читают так: чтобы из вектора