КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Векторами в координатной форме
.2.1. Декартов ортонормированный базис
Определение.Векторы  образуют правую тройку векторов, если из конца вектора
образуют правую тройку векторов, если из конца вектора  кратчайший поворот от вектора
кратчайший поворот от вектора 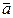 к вектору
к вектору 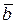 виден против часовой стрелки и левую тройку векторов, если кратчайший поворот виден против часовой стрелки.
виден против часовой стрелки и левую тройку векторов, если кратчайший поворот виден против часовой стрелки.

|
 
| Векторы  на рис.4 образуют левую тройку векторов,
на рис.5 на рис.4 образуют левую тройку векторов,
на рис.5  правую тройку. правую тройку.
|
Определение.Если в 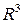 задан базис
задан базис 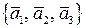 где
где  попарно взаимно перпендикулярны, то базис называется ортогональным. Если
попарно взаимно перпендикулярны, то базис называется ортогональным. Если  и
и  , то базис называется ортонормированным. Если векторы
, то базис называется ортонормированным. Если векторы  попарно взаимно перпендикулярны,
попарно взаимно перпендикулярны,  и
и  образуют правую тройку векторов, то базис называется декартовым ортонормированным.
образуют правую тройку векторов, то базис называется декартовым ортонормированным.
Определение.Если в трехмерном пространстве заданы: 1) произвольная точка О  начало отсчета и 2) декартов ортонормированный базис
начало отсчета и 2) декартов ортонормированный базис  то говорят, что в пространстве задана декартова прямоугольная система координат. В дальнейшем, если не оговорено специально, будем использовать
то говорят, что в пространстве задана декартова прямоугольная система координат. В дальнейшем, если не оговорено специально, будем использовать
сокращенную запись  ДСК.
ДСК.
Прямые, проходящие через начало координат, называются осями координат: ОХ  ось абсцисс; OY
ось абсцисс; OY  ось ординат; OZ
ось ординат; OZ  ось аппликат.
ось аппликат.
Векторы  ,
, 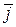 ,
, 
 называются координатными ортами.
называются координатными ортами.
 координатная прямая
координатная прямая
|  система координат
на плоскости
система координат
на плоскости
| 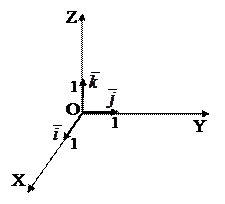 система координат
в пространстве
система координат
в пространстве
|
Дата добавления: 2014-11-13; просмотров: 236; Мы поможем в написании вашей работы!; Нарушение авторских прав |