
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства смешанного произведения.
10.  , т.е. смешанное произведение не меняется при циклической перестановке векторов. , т.е. смешанное произведение не меняется при циклической перестановке векторов.
|
20.  , т.е. смешанное произведение не меняется при перестановке знаков векторного и скалярного произведения. , т.е. смешанное произведение не меняется при перестановке знаков векторного и скалярного произведения.
|
30.  , т.е. смешанное произведение меняет знак при перестановке любых двух векторных сомножителей. , т.е. смешанное произведение меняет знак при перестановке любых двух векторных сомножителей.
|
40.Теорема 5. Если в ДСК заданы векторы  , , 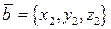 , ,  то то  .
Дано: .
Дано:  , , 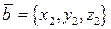 , ,  Доказать:
Доказать:  .
Доказательство.По определению .
Доказательство.По определению 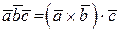 . Найдем . Найдем  . .
 . Тогда теореме 2. . Тогда теореме 2.  

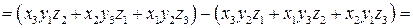  .
Замечание. Если .
Замечание. Если  образуют правую тройку векторов, то образуют правую тройку векторов, то  ,
если ,
если  левую тройку, то левую тройку, то  . .
|
50.Теорема 6.Для того, чтобы векторы  были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю, т.е. были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю, т.е.  . Докажем эту теорему.
1) Необходимое условие.
Дано: . Докажем эту теорему.
1) Необходимое условие.
Дано:   компланарны, компланарны,  , , 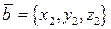 , ,  Доказать:
Доказать:  .
Доказательство.Из определения компланарности следует, что векторы .
Доказательство.Из определения компланарности следует, что векторы  лежат в одной плоскости, тогда один из векторов, например, лежат в одной плоскости, тогда один из векторов, например, 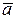 линейно выражается через векоры линейно выражается через векоры 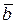 и и  , т.е. , т.е.  . Тогда в определителе из координат векторов строки линейно зависимы. Следовательно, определитель равен нулю. Это означает, что . Тогда в определителе из координат векторов строки линейно зависимы. Следовательно, определитель равен нулю. Это означает, что  , ч.т.д.
2) Достаточное условие.
Дано: , ч.т.д.
2) Достаточное условие.
Дано:  . .  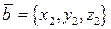  Доказать:
Доказать:   копланарны.
Доказательство.Если копланарны.
Доказательство.Если  , то определитель из координат векторов равен нулю , то определитель из координат векторов равен нулю 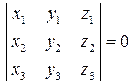 . Из этого следует, что строки определителя линейно зависимы. Тогда векторы так же линейно зависимы, например, . Из этого следует, что строки определителя линейно зависимы. Тогда векторы так же линейно зависимы, например,  . Это возможно, лишь в случае, когда векторы . Это возможно, лишь в случае, когда векторы  лежат в одной плоскости, т.е. компланарны, ч.т.д. лежат в одной плоскости, т.е. компланарны, ч.т.д.
|
Дата добавления: 2014-11-13; просмотров: 238; Мы поможем в написании вашей работы!; Нарушение авторских прав |