
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Связь между составляющей и проекцией
Пусть на оси  задан вектор задан вектор  единичной длины (орт), идущий по положительному направлению оси единичной длины (орт), идущий по положительному направлению оси  , ,   проекция вектора проекция вектора 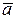 на ось на ось  , ,  составляющая вектора составляющая вектора 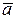 на ось на ось  . .
| |
 1. 1.
| Вектор  , следовательно , следовательно
 . .
|
 2. 2.
| Вектор  , следовательно , следовательно
 . .
|
 3. 3.
| Так как  , следовательно , следовательно  , ,
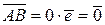 . .
|
| Составляющая вектора на ось есть вектор равный произведению проекции вектора на ось на орт направления. |
2.4. Координаты вектора в ДСК
Вектор  , ,  , тогда , тогда  ,
т.е. ,
т.е.  . Проекции вектора на координатные оси равны: . Проекции вектора на координатные оси равны:

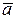 на оси: на оси:  , тогда , тогда  . Выражение . Выражение 
называется разложением вектора
| ||||
Замечания:
 координатные орты координатные орты  имеют координаты имеют координаты    ; ;
 векторы векторы  , ,  , ,  удовлетворяют условиям:
1) векторы удовлетворяют условиям:
1) векторы  попарно перпендикулярны; 2) векторы попарно перпендикулярны; 2) векторы  линейно независимы так как линейно независимы так как  . Следовательно, векторы . Следовательно, векторы  , ,  , ,  образуют ортонормированный базис трехмерного пространства; образуют ортонормированный базис трехмерного пространства;
 любой вектор любой вектор  разлагается по базису разлагается по базису  единственным
образом: единственным
образом: 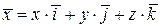 . .
|
Дата добавления: 2014-11-13; просмотров: 268; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 , где
, где  называютсякоординатами вектора
называютсякоординатами вектора  или
или  . В дальнейшем будем использовать запись
. В дальнейшем будем использовать запись