Метод прямого измерения производной

Этот метод основан на том, что для измерения производной можно измерять производные dJ/dt и du/dt, а затем находить нужную величину делением:

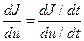. (7.3)

Этот метод не требует использования поискового сигнала, однако в процессе дифференцирования возможно накопление ошибок. Структурная схема такой экстремальной системы приведена на рис. 7.2а.

Релейный элемент в системе в зависимости от знака производной обеспечивает запуск и реверс исполнительного механизма, который и обеспечивает изменение показателя качества в сторону экстремума. В точке экстремума dJ/du=0 и движение к экстремуму должно остановиться, но процесс адаптации на этом не заканчивается. Дело в том, что экстремальная зависимость может непрерывно изменяться из-за дрейфа параметров объекта, флуктуационных шумов и др., поэтому система должна находиться в непрерывном движении, а, кроме того, важно, чтобы система не «застряла» в точках побочного экстремума случайного характера (помехах). Поэтому используемое реле имеет зону гистерезиса полушириной и движение из исходной точки М₁ характеристики в область экстремума происходит так, как это изображено на рис. 7.2б.

а	б
Рис. 7.2. Поиск экстремума методом прямого определения производной. а – структурная схема экстремальной системы: ОУ – экстремальный объект управления, ИМ – исполнительный механизм (обычно интегрирующее звено), БД – блок деления; б – графики временных зависимостей сигналов в экстремальной системе в процессе поиска экстремума (установившийся режим рыскания).

Для оценки величины потери на рыскание и максимального отклонения показателя качества от экстремального значения положим, в первом приближении, что статическая характеристика имеет вид параболы. Можно показать, что в этом случае величины максимального отклонения, периода рыскания и потерь на рыскание выражаются соотношениями:

(7.4)