Обучение детей делению целого предмета на равные части

Программой предусмотрено научить детей делить предмет на две, четыре, восемь, три, шесть, пять, семь равных частей (напри­мер, разделить яблоко, булку, лист бумаги и т. д.), называть эти части (половина или одна вторая, одна четвертая, две (три) чет­вертых, одна восьмая, две (три... семь) восьмых, одна третья, две третьих и т. д.), на конкретном материале устанавливать, что це­лое больше части, а часть меньше целого.

Зачем введена эта программная задача? Что дает она для ум­ственного и в частности математического развития ребенка до­школьного возраста? Так ли уж необходимо ее включение в «Про­грамму»?

Да, необходимо. Обучение детей делению целого предмета на несколько равных частей позволит выявить ряд закономерностей в вещах и явлениях, скрытых для непосредственного восприятия, поможет формированию логического мышления детей, умению находить причинные связи, судить по итогу об исходных данных, словом, даст широкий общеразвивающий эффект.

Обучение детей делению целого на равные части тесным обра­зом связано с измерением величин условной меркой, и все выше­сказанное о широком общеразвивающем эффекте в полной мере относится и к обучению детей измерению. Но в связи с тем, что в программе темы эти разъединены и одна из них («Деление це­лого на равные части») помещена в рубрику «Количество и счет», а другая («Измерение»)- в рубрику «Величина», мы разберем эти темы отдельно, останавливаясь, разумеется, и на точках их пересечения.

Умение делить целое на равные части позволяет решить и ряд практических задач, когда в жизни (в том числе и в детской) воз­никает необходимость деления конкретного предмета (например, яблока) на две или четыре одинаковые части.

И наконец, обучение детей делению целого на несколько рав­ных частей позволит в какой-то мере избежать существующий до настоящего времени недостаток математического развития детей, в частности их отношение к единице. Проверка знаний воспитан­ников детских садов показывает, что дети считают только пред­меты, стоящие отдельно друг от друга, и не могут сосчитать два предмета за один, если образцом для счета являются два пред­мета.

Так, мы предлагали ребенку внимательно следить за нашими действиями — считать, сколько крупы мы насыпали. А насыпали мы в кучку на столе две столовые ложки риса. Затем передавали ту же ложку ребенку и просили его сделать пять раз по стольку же или пять таких же кучек (пять кучек, из двух ложек крупы каждая). Подавляющее большинство детей с заданием не справ­лялось: они насыпали или пять кучек, но по одной ложке, или на­сыпали пять ложек в одну кучку.

Что дает нам для устранения этого недостатка, ограничиваю­щего возможности счета, деление целого предмета на несколько равных частей? Представьте себе: в руках у воспитателя (а затем и у детей) прямоугольный лист бумаги. Воспитатель, обращая на него внимание, спрашивает: «Сколько у меня листов бумаги?» «Один», — отвечают дети. Затем воспитатель сгибает бумагу, де­лит ее пополам: «Сколько листочков получилось?» «Два», —го­ворят дети. «А если я сложу эти листочки так, как было до деле­ния, — продолжает воспитатель и складывает части по линии раз­рыва, — что получится?» — «Один лист бумаги».

Дети сумели объединить два отдельных листочка бумаги в один и обозначить это соответствующим словом. За единицу приняты, по существу, два предмета.

При последующем обучении детей делению целого на равные части, измерению с помощью условной мерки эта задача будет уточняться, уясняться детьми, и к концу дошкольного периода у них должно быть сформировано полноценное понятие о числе.( Вся работа по делению целого на равные части в детском саду ведется обязательно на конкретном материале, что предусмотрено и программой.)

Теперь перейдем к конкретным рекомендациям, которые могут помочь воспитателям в проведении занятий.

Мы уже говорили о том, что детей очень важно заинтересовать решением той или иной задачи, сделать необходимым поиск путей этого решения. Поэтому на первом занятии воспитательница соз­дает игровую' ситуацию. Например, на столе у педагога стоят ку­кольный стол и стул. Больше ничего. Воспитательница говорит, что ждет в гости куклу Наташу. Приходит Наташа. Воспитатель­ница ставит перед ней. тарелку. Вскоре приходит кукла Лена. Но у воспитательницы только один кусок пирога. Дети предлагают разные решения, и, наконец, один наиболее приемлемый — разде­лить пополам. Воспитательница разрезает пирог на две равные части и кладет на тарелки Лене и Наташе.

Введение в деление целого предмета на две равные части про­изошло. Теперь надо упражнять детей в этом. Воспитательница показывает, как разделить пополам яблоко. Делит, сравнивает половины, показывает, что они одинаковые, равные. То же самое она делает с конфетой и печеньем, но при делении конфеты и пе­ченья воспитательница не только обращает внимание детей на то, сколько кусочков получилось и одинаковые ли они, но и говорит детям, что кусочки по-другому называются частями.

При этом воспитательница вновь и вновь показывает детям кусочки печенья или конфеты, .подчеркнуто сравнивает их, говоря: «Одинаковые, равные части». Постепенно эти определения войдут в активный словарь детей.

Первое занятие, как мы уже говорили, является введением в тему деления целого на равные части, и поэтому очень важно на первом занятии показать, как делятся пополам самые разнообраз­ные предметы.

С этой целью (после того как куклы «поели») воспитательница ставит на стол две чашечки и маленькую бутылку с соком. Зара­нее (до занятия и без детей) она измерила, сколько надо налить сока, чтобы получилось две полные чашки (ни больше, ни мень­ше).

Если наличие чашек на столе не поможет детям найти способ деления жидкости на две равные части, воспитательница покажет его сама, разливая сок по чашкам и обращая внимание детей на равное количество сока в той и в другой. При этом так же необ­ходимо говорить детям, что сок разделили пополам, на две равные части.

Что еще хорошо разделить на этом занятии? Какие-либо пред­меты, которые делятся путем сгибания.

Воспитательница показывает детям ленту. Она одна. И приго­товлена была в подарок Наташе. Но пришли две девочки. «Что же кадет сделать, чтобы подарить ленту и той и другой?» Воспитательница складывает ленту пополам и обращает на это внимание детей, затем разрезает ленту и завязывает бантики Лене и Наташе.

«Нашим куклам хочется порисовать, но у меня опять приготов­лен только один лист бумаги. Что делать?»—спрашивает воспи­тательница.

Пусть дети попробуют оформить в слове только что получен­ный опыт: «Нужно разделить лист бумаги пополам, получатся две равные части, одну часть, или половину, надо дать Наташе, дру­гую — Лене». Воспитательница проделывает все то, о чем только

- что говорили дети.

«А теперь вы,— обращается воспитательница к детям,— разде­лите на две равные части листочки бумаги, которые лежат у вас на столе».

Дети делят. Воспитательница следит, как дети действуют, помогает сложить точно посередине, чтобы концы совпали с концами, -' и только тогда разрешает разрезать или разорвать листочки.

После этого воспитательница просит их показать одну часть. Дети поднимают листочек. Воспитательница просит показать две части. Дети показывают. Затем предлагает положить листочек на листочек (или часть на часть) и уточняет с детьми, что части по­лучились равные, одинаковые. На этом первое занятие может быть закончено.

Мы подробно остановились на его описании, так как правильно проведенное первое занятие — залог дальнейшего успеха. Остальные занятия в той или иной мере связаны с первым и, по существу, расширяют и уточняют знания, полученные детьми.

Первое занятие посвящено целиком одной программной зада­че — делению целого предмета на две равные части. В последую­щие занятия будут включаться и другие задачи: на развитие пред­ставлений о величине, форме предметов, на уточнение знаний о количестве, числе, счете и т. д. Может быть две, три, четыре, а го и пять программных задач, в зависимости от насыщенности заня­тия и от того, насколько усвоена новая задача.

Куклы на занятии должны быть одинаково привлекательны. (У нас был случай, когда дети делили не поровну лишь потому, что одна из кукол была красивее, опрятнее, наряднее другой, и ребята все норовили ей дать получше да побольше кусочек.) Если же все-таки дети скажут, что надо разделить яблоко, но не ука­жут, что поровну, воспитательница должна разделить не поровну и, -показав детям неодинаковые кусочки, спросить, какой кукле дать меньше. Обычно дети говорят: «Вы неправильно разделили. Надо было пополам». Таким образом, они сами делают вывод о необходимости деления на равные части, а это полезнее, чем

сооб­щение воспитателя, не подкрепленное детским опытом.

Иногда воспитательница, усадив кукол за стол, говорит с сожа­лением, что угощение приготовлено для одной. При этом она кла­дет на поднос сразу все продукты: хлеб, яблоко, печенье, конфе­ту, апельсин. И дети, помня об указании воспитателя делить все пополам, предлагают: «Наташе — апельсин и конфету. Она раньше пришла. Лене - яблоко и печенье. А хлеб пусть пока полежит».

Естественно, воспитательница бывает удивлена, хотя сама на­толкнула детей на такое решение. Поэтому в начале занятия все угощение должно лежать в вазе (или на подносе), покрытое сал­феткой, и доставать нужно по одному предмету, побуждая детей делить их последовательно (как задумано нами).

Проводя первое занятие (как и любое другое), воспитательни­ца должна помнить о главной задаче, стоящей перед ней. В нашем примере главное — математика, вернее, один из ее моментов: це­лое и часть, поэтому на уяснение детьми данного содержания и должно быть направлено все занятие, в том числе и игровая ситуа­ция.

Однако нередко воспитательница (из самых добрых побужде­ний), если дети не скажут, что делить надо поровну, использует, на ее взгляд, подходящую ситуацию и начинает поучать, как надо обращаться с гостями, когда они приходят в дом.

Во время самостоятельного деления детьми целого предмета на равные части воспитателю необходимо обращать внимание на технику выполнения задания. Если дети умеют разрывать бумагу по сгибу, они должны это делать и на занятиях математикой. Же­лательно иметь специальные ножи для разрезания бумаги и на­учить детей ими пользоваться. Если их нет, нужно давать ножни­цы, но и в том, и в другом, и в третьем случае необходимо следить за тем, чтобы дети разрезали (или разрывали) лист точно по ли­нии сгиба, так как только при этом условии можно разделить его пополам. Иногда дети разрезают неровно и потом, стараясь, чтобы этого не заметил воспитатель, «лишние» кусочки стремятся ото­рвать и спрятать. В результате получается, что ребенок разделил не тот лист, который ему дали, а меньший, и части у него полу­чатся меньше, чем у соседа.

И еще один момент, на который воспитательница постоянно должна обращать свое внимание и внимание детей, -

это речь воспитанников. Дети обычно говорят, что разделить надо не попо­лам, а на пополам, и части у них получаются не равные, а ровные. Обогащать словарь детей, уточнять его важно не только для пра­вильного речевого, но и математического развития: точная наука требует столь же точного обозначения тех представлений, кото­рыми ребенок оперирует.

На втором занятии воспитательница может повторить содер­жание, первого, но взять других кукол, другое угощение. Нужно обратить большее внимание на активизацию словаря детей. Для самостоятельной работы можно предложить круги из бумаги. На этом занятии будет еще одна или две программные задачи из дру­гих разделов.

На третьем занятии воспитательница показывает детям прин­цип деления целого предмета на четыре равные части (например, на яблоке, булке, прямоугольном и круглом листе бумаги), скла­дывая листы бумаги пополам и еще раз пополам. Дети делят толь­ко бумагу прямоугольной и круглой формы, используя тот же при­ем сгибания пополам.На этом, третьем, занятии воспитатель ставит еще одну цель- показать детям, как часть относится к целому: часть меньше це­лого, а целое больше своей части. Для этого воспитательница раздает детям по два листа одной и той же формы. Один лист дети делят, другой (целый) остается нетронутым. Затем воспита­тельница просит показать одну из четырех частей. Дети показы­вают. Потом нужно предложить им показать целый лист. Дети вы­полняют задание. В руках у них оказывается одна 'часть и целый лист. Воспитательница предлагает сравнить и сказать, какой из листочков больше — часть или целое.

Кроме этой программной задачи, в третье занятие так же как и во все последующие, будут включены задачи и из других разде­лов математики.

Названия частей: одна вторая, одна, две, три четвертых и т. д.— должны быть обязательно поняты детьми, в противном случае пользоваться ими не следует. Дети должны понять, а воспитатель­ница— им разъяснить на наглядном материале, что один (любой) листочек бумаги из четырех (если бумага разделена на четыре равные части) называется одной частью. И с самого начала вос­питатель просит показать одну часть из четырех, добиваясь, чтобы дети показали каждую из четырех частей.

«Теперь покажите две части из четырех, три части из четырех». Дети, выполняя задание, берут каждый раз соответствующее ко­личество и предъявляют воспитательнице. То же самое они де­лают и при делении предмета на любое количество частей.

«Теперь, — говорит воспитательница, — я скажу немного по-другому, а вы подумайте, что надо показать. Покажите одну чет­вертую. Покажите три четвертых».

После такого объяснения ни один ребенок не ошибается, а тер­минология приобретает необходимую четкость и соответствие с об­щепринятыми названиями.

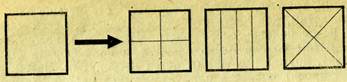
На четвертом занятии можно предложить делить уже знакомую форму — круг — на четыре равные части и новую — треугольник (прямоугольный, равнобедренный — его удобнее всего складывать пополам, угол к углу — он получается при делении квадрата по диагонали), а также упражнять детей в различении одной четвер­той, двух четвертых и т. д.

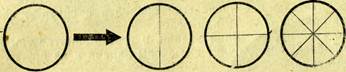
На этом же занятии следует показать детям разные способы деления квадрата и круга на четыре равные части, уточняя каж­дый раз, какой формы получаются части, сколько их всего, как они называются (см. рис. 11 и 12).

Рис.11

Рис.12.

Продолжая учить детей делению предмета на равные части, можно на пятом занятии, пользуясь тем же приемом, что и при делении на две и четыре части, т. е. путем сгибания пополам и еще пополам, показать детям деление на восемь равных частей. Так дети делят листки бумаги прямоугольной, квадратной, круг­лой, треугольной форм. В ответ на просьбу воспитательницы они будут показывать одну восьмую, пять восьмых и т. д.; сравнивать части и целое, определяя каждый раз, что целое больше своей части, а часть меньше целого, от деления которого она образована. Необходимо также каждый раз обращать внимание детей и на то, что все части, полученные при делении предмета на то или иное количество равных частей, одинаковые, равны между собой. Пусть дети сравнивают, накладывая часть на часть.

Итак, дети научились делить предметы на две, четыре, восемь равных частей. Теперь очень хорошо научить по части находить целое и, наоборот, по целому его часть. С этой целью воспитатель­ница на шестом или седьмом (как получится) занятии предлагает детям разделить лежащие перед ними прямоугольные листочки бумаги на четыре равные части. Сама она тоже берет лист бума­ги прямоугольной формы, но несколько меньших размеров и делит его на четыре равные части. Затем воспитательница просит детей показать одну четвертую их листа. Дети выполняют задание. Тог­да воспитательница показывает одну четвертую своего листа и обращает внимание на разницу в размере: у детей листочек, на­зывающийся одной четвертой, больше листочка с тем же назва­нием у воспитательницы. Почему? Не спешите ответить сами. Пусть подумают ваши воспитанники, а вы помогите им прийти к выводу, что целые листы .были неодинаковые, что лист, который делили они, был больше листа, который делили вы. И тогда обя­зательно покажите им приготовленные заранее дубликаты бумаги. Дети сравнивают целые листы. После этого предложите им при­ложить к каждому из листов соответствующие четвертые части-. Таким образом дети будут учиться видеть взаимосвязь и взаимо­зависимость явлений — весьма важный момент в развитии их ло­гического мышления.

Чтобы дети увидели, что четыре четвертые части (две вторые, восемь восьмых и т. п.) действительно составят одно целое, вос­питательница раздает детям два совершенно одинаковых по фор­ме и величине листа бумаги. Один из них предлагает разделить на четыре равные части. После деления и просьбы показать одну, две, три и четыре четвертых воспитатель спрашивает: «Как можно по-другому назвать четыре четвертых?» Если дети не знают, им предлагается положить четыре четвертых на целый лист так, что­бы его не было видно. Дети выполняют задание и наглядно убеж­даются в том, что четыре четвертых и целый даст — одно и то же и что четыре четвертых по-другому можно назвать один целый лист.

Мы говорили о делении предметов, которые можно сложить пополам. А как быть в том случае, если предмет надо разделить тоже на две или четыре равные части, а сложить его при этом не­возможно (кусок фанеры, плотного картона и т. д.)? Каким спо­собом должен овладеть ребенок, чтобы разделить такой предмет? Измерением.

Воспитательница (примерно на восьмом занятии) рисует на доске удлиненный невысокий прямоугольник и предлагает детям подумать, как можно этот прямоугольник разделить на четыре равные части.' На столе у воспитательницы лежит шнурок, равный длине прямоугольника, нарисованного на доске.

В результате наводящих вопросов («Чем можно измерить пря­моугольник?», «Как можно разделить шнурок?», «Какую можно выбрать мерку?») дети должны прийти к решению: надо взять шнурок, измерить им прямоугольник, убедиться, что части равны по длине, затем шнурок сложить пополам и еще раз пополам. По­лучившийся сложенный шнурочек отложить четыре раза на пря­моугольнике, сделать мелом отметки. Мы разделили прямоуголь­ник, нарисованный на доске, на четыре равные части, каждая из этих частей называется одной четвертой. Разумеется, ничего этого сразу дети не скажут, и не надо заставлять их учить наизусть такие длинные объяснения. Все это воспитатель покажет сам, гово­рить будет вместе с детьми, и только в результате ряда подобных упражнений они поймут суть проделанных операций и научатся к концу года правильно формулировать уже произведенные дейст­вия.

Считаем необходимым остановиться на поддержании интереса детей на занятии и мотивации их деятельности.

Ребенку интересно знать, для чего он выполняет то или иное действие. Такая далекая цель, как успешная учеба в школе, не очень осязаема для ребенка. Заманчивым должно быть конкрет­ное занятие, и интерес активизирует мышление, способствует вос­питанию необходимых качеств умственной деятельности.

Приведем в качестве примера случай, произошедший на по­следнем из описанных выше занятий. На предложение педагога подумать, как можно вот такой нарисованный прямоугольник раз­делить на четыре равные части, дети ответили мимолетной вспыш­кой интереса и молчанием. Трудно. Так еще никогда не делили. Трудно и неинтересно: ну, для чего его нужно делить? Дети стали отвлекаться. Занятие срывалось. И тогда воспитательница решила составить коротенький рассказ.

«Сережа жил в деревне у дедушки с бабушкой. В саду у них был большой стол, за которым в хорошую погоду собиралась вся семья. Однажды дедушка сказал: «Давно я хочу сделать к столу новые ножки, да все откладываю. Но сегодня мы можем с тобой этим заняться». Сережа радостно спросил: «Значит, я буду тебе помогать?;» — «Конечно», — ответил дедушка. Они пошли в угол сада, где у дедушки было запасено длинное тонкое бревно. «Нам нужно разделить его на четыре части», — сказал дедушка. «А как же это сделать?» — спросил Сережа. «Подумай», — ответил дедуш­ка и положил рядом с бревном веревку, равную его длине. Сережа задумался.

А мы давайте ему поможем. Представьте, что прямоугольник, нарисованный на доске, совсем не прямоугольник, а бревно. Как его разделить на четыре равные части?»

Дети оживились: теперь была цель, ради которой надо было думать. Предложения поступали разные, но нужного решения не было. Воспитательница взяла в руки шнур, и тогда очень тихая девочка Ира подняла руку: «Я не знаю, как сказать, но можно я покажу?» — «Пожалуйста». Ира подошла к доске, взяла шнур, приложила его к прямоугольнику. Длина совпала. И тут все дети поняли. Они наперебой предлагали правильное решение задачи. Нам кажется этот пример весьма показательным. К делению цело­го на равные части воспитательница будет обращаться еще не раз в течение года; конечно, не на каждом занятии, но периодически •включать в план эту программную задачу необходимо. Показывая детям лист бумаги, можно предложить им вообразить, что это кусок белого шелка или пачка мороженого, и их нужно разделить между тремя-четырьмя детьми.

На последующих занятиях шнурок, лента, веревочка или узкая полоска бумаги, которыми дети будут мерить объект, подлежащий делению на несколько равных частей, даются не только равными протяженности объекта, но и длиннее его. Дети же должны вна­чале установить, какую длину им нужно делить, отложить ее на шнурочке, т. е. заметить то место, которое соответствует длине измеряемого предмета, и только тогда действовать описанным вы­ше способом(Рис.13)

Рис.13

Кроме того, необходимо показать наиболее удобные приемы де­ления. Например, прямоугольный лист бумаги удлиненной формы удобнее делить на две, четыре или восемь равных частей: