
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Amp; Методичні вказівки. Найбільш «логічним» типом міркувань є дедуктивні умовиводи, оскільки вони дають повністю обґрунтовані засновками висновки
Найбільш «логічним» типом міркувань є дедуктивні умовиводи, оскільки вони дають повністю обґрунтовані засновками висновки. Правильним дедуктивним умовиводом називають таке міркування, яке у підсумку не додає інформації, а тому забезпечує отримання істинного висновку з істинних засновків. Тобто, у правильному дедуктивному умовиводі між засновками і висновком повинно існувати відношення логічного слідування, тобто таке відношення, у якому за наявності істинних засновків висновок не може бути помилковим.
Розгляд дедуктивних міркувань зазвичай починають з найпростіших, безпосередніх умовиводів, до складу яких входить один засновок, який є категоричним судженням. У безпосередньому умовиводі висновок можна отримати двома шляхами: 1) через відношення суджень (за логічним квадратом); 2) через перебудову структури суджень.
Умовиводами за логічним квадратом є усі переходи по логічному квадрату, коли істинність або хибність одного судження з необхідністю вказує на певне істиннісне значення іншого. Перевірка їх правильності полягає у співставленні істиннісного значення висновку з тим, що йому зумовлене логічним відношенням із засновком.
Приклад. З істинності висловлювання: «Не всі книги є цікавими» слідує хибність висловлювання «Жодна книга не є цікавою». Перше висловлювання частковостверджувальне, друге, – загальнозаперечне. За логічим квадратом вони перебувають у відношенні контрадикторності, правилом якого є те, що два супуречливих судження не можуть бути одночасно істинними або одночасно хибними, якщо одне з них істинне, то інше обов’язково – хибне (і навпаки).
З чотирьох порівнянних суджень за логічним квадратом, два завжди будуть істинними, а два – хибними.
Безпосередні умовиводи, які виникають шляхом перебудови структури судження, засновані на тому, що відношення суб’єкта і предиката у засновку має обумовлювати відношення термінів висновку. Для перебудови структури судження існують два основних способи – перетворення і обернення, які можна поєднувати в тому або іншому порядку і отримувати складніші типи зміни структури судження – протиставлення предикату і протиставлення суб’єкту.
Перетворення судження полягає в еквівалентній перебудові судження шляхом зміни його якості, тобто стверджувальне судження стає заперечним, а заперечне – стверджувальним. Проте, щоб перетворення було еквівалентним, окрім зміни якості судження, його предикат має бути замінений на суперечне поняття. Таким чином, «Усі S є Р» перетворюється у «Жодне S не є не-Р», «Деякі S є Р» перетворюється на «Деякі S не є не-Р», «Жодне S не є Р» перетворюється на «Усі S є не-Р», а «Деякі S не є Р» перетворюється на «Деякі S є не-Р».
Приклад: Усі вовки (S) – хижі тварини (Р) – (А)
Жоден вовк (S) не є не хижою твариною (не-Р) – (Е)
Обернення судження здійснюється перестановкою суб’єкта і предиката при дотриманні правила, що нерозподілений спочатку термін не може виявитися розподіленим у результаті перетворення. Дотримання цього правила накладає обмеження на цю операцію, так що в одних випадках оберненняможе відбуватися чисто, без зміни кількості судження, – так обертаються частковостверджувальні та загальнозаперечні судження (просте обернення). У інших випадках воно відбувається з обмеженням (зменшення кількості судження) – так обертаються загальностверджувальні судження (обернення з обмеженням). У деяких випадках воно взагалі неможливе – для частковозаперечних суджень. Отже, «Усі S є Р» обертається у «Деякі Р є S», «Деякі S є Р» обертається на «Деякі Р є S», «Жодне S не є Р» обертається на «Жодне Р не є S».
Приклад: Жоден плазун (S) не літає (Р) – (Е)
Жоден з літаючих (Р) не належить до плазунів (S) – (Е)
Для протиставлення предикату потрібно спочатку зробити перетворення і результат обернути. Приклад:
Жодна планета (S) не є зіркою (Р) – (Е)
Усі планети (S) є не-зірками (не-Р) – (А)
Деякі не-зірки (не-Р) є планетами (S) – (І)
Для протиставлення суб’єкту треба виконати ці операції у зворотному порядку.
Перевірка правильності таких умовиводів здійснюється або відтворенням відповідних операцій і порівнянням їх результату з наявним висновком, або графічно. Для перевірки першим способом треба визначити, яка імовірно операція здійснювалася. Побачити перетворення або обернення нескладно. При протиставленні предикату на місці суб’єкта виявляється поняття, що суперечить предикату, а на місці предиката – суб’єкт вихідного судження. При протиставленні суб’єкту на місці суб’єкта виявляється предикат вихідного судження, а на місці предиката – поняття, що суперечить суб’єкту вихідного судження.
З частковостверджувального судження типу І при протиставленні необхідні висновки не випливають: 1. Деякі S є Р (І); 2. Деякі S не є не-Р (О); 3. Судження типу О не обертаються.
«Винахід силогістичної форми є одним з найпрекрасніших і навіть найважливіших відкриттів людського духу» (Г.В. Ляйбніц).
Простий категоричний силогізм (ПКС) – це вид дедуктивного умовиводу, що складається з двох засновків і висновку, які є категоричними судженнями.
Приклад:
Усі ссавці (М) дихають легенями (Р) – більший засновок
Усі кити (S) – ссавці (М) – менший засновок
Усі кити (S) дихають легенями (Р) – висновок
Поняття, що входять до складу силогізму, називаються термінами силогізму. Меншим терміном називається суб’єкт висновку і позначається S. У нашому прикладі менший термін – кити. Засновок, який містить у собі менший термін, називається меншим засновком. Більшим терміном називається предикат висновку і позначається як Р. У нашому випадку – дихають легенями (S і Р називаються ще крайніми термінами). Засновок, який містить у собі більший термін, називається більшим засновком. Середнім терміном називається термін, якого немає у висновку, але який є в обох засновках, що забезпечує логічний зв’язок між засновками. Позначається як М – ссавці.
Правила силогізму поділяються на загальні та правила фігур (спеціальні). Загальні правила силогізму застосовані до усіх простих силогізмів, незалежно від того, за якою фігурою вони побудовані. Спеціальні правила діють тільки для кожної фігури силогізму і тому часто називаються правилами фігур. Загальних правил категоричного силогізму існує всього сім: три з них – це правила термінів, чотири – правила засновків.
Загальні правила силогізму
1. У силогізмі повинно бути лише три терміни. Приклад:
Рух вічний.
Ходіння до університету – рух.
=> Ходіння до університету вічне.
Обидва засновки цього силогізму є істинними судженнями, проте з них випливає помилковий висновок, тому що порушено дане правило. Слово рух вживається у двох засновках у двох різних значеннях: рух як філософська категорія і рух як фізична дія. Тому, термінів у силогізмі три: рух, ходіння до університету, вічність; а значень (оскільки один з термінів вживається у двох різних значеннях) чотири, тобто зайве значення має на увазі зайвий термін. У наведеному прикладі силогізму було не три, а чотири (за значенням) терміни. Помилка, що виникає при порушенні наведеного вище правила, називається почетверінням термінів.
2. Середній термін має бути розподілений хоч б в одному із засновків. Повне коло (за схемою Ейлера) означатиме розподілений термін (+), а неповне – нерозподілений (-). Приклад:
| Усі кішки (К) – це живі істоти (ж. і). Сократ (С) – це теж жива істота. => Сократ – це кішка. | 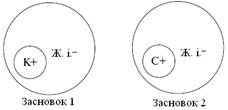
|
З двох істинних засновків отримуємо помилковий висновок. Зображуємо колами Ейлера відношення між термінами у засновках силогізму і встановлюємо розподіленість цих термінів.
Середній термін (живі істоти) у даному випадку нерозподілений у жодному із засновків, а за правилом він має бути розподілений хоч б в одному. Помилка, що виникає при порушенні даного правила, так і називається – нерозподіленість середнього терміну у кожному засновку.
3. Термін, який був нерозподілений у засновку, не може бути розподілений у висновку. Приклад:
| Усі яблука (Я) – їстівні предмети (Ї. п.). Усі груші (Г) – це не яблука. => Усі груші – неїстівні предмети. | 
|
Засновки силогізму є істинними судженнями, а висновок – заперечний. Зображуємо колами Ейлера відношення між термінами у засновках і у висновку силогізму та встановлюємо розподільність цих термінів.
У даному випадку предикат висновку, або більший термін силогізму (їстівні предмети),у першому засновку є нерозподіленим (-), а у висновку – розподіленим (+), що забороняється даним правилом. Помилка, що виникає при його порушенні, називається розширенням більшого терміну.
4. У силогізмі не повинно бути двох заперечних засновків. Хоч б один із них має бути стверджувальним (можуть бути стверджувальними і обидва засновки). Якщо два засновки у силогізмі заперечні, то висновок з них або взагалі зробити не можна, або ж, якщо його зробити можливо, він буде помилковим або, принаймні, недостовірним, імовірним. Приклад:
Снайпери не можуть мати поганого зору.
Усі мої друзі – не снайпери.
=> Усі мої друзі мають поганий зір.
Обидва засновки у силогізмі є заперечними судженнями, і, незважаючи на їх істинність, з них отримуємо помилковий висновок. Помилка, яка виникає у даному випадку, так і називається – два заперечних засновки.
5. У силогізмі не повинно бути двох часткових засновків.
Хоч б один із засновків має бути загальним (можуть бути загальними і обидва засновки). Якщо два засновки у силогізмі є частковими судженнями, то висновок з них зробити неможливо. Приклад:
Деякі філософи – матеріалісти.
Деякі філософи – ідеалісти.
=>?
З цих засновків ніякого висновку отримати неможливо, тому що обидва вони є частковими. Помилка, що виникає при порушенні цього правила, так і називається – два часткових засновки.
6. Якщо один із засновків заперечний, то і висновок має бути заперечним.
Приклад:
Усі травоядні живляться рослинною їжею.
Усі тигри не живляться рослинною їжею.
=> Усі тигри не є травоядними.
З двох засновків цього силогізму не можна отримати стверджувальний висновок. Він може бути виключно заперечним.
7. Якщо один із засновків частковий, то і висновок має бути частковим.
Приклад:
Усі олімпійські чемпіони є спортсменами.
Деякі українці – це олімпійські чемпіони.
=> Деякі українці – це спортсмени.
У цьому силогізмі з двох засновків неможливо отримати загальний висновок. Він може бути лише частковим, оскільки другий засновок є частковим.
Аксіома силогізму є віддзеркаленням багатовікової практики людей, мільярдного повторення однієї й тієї ж розумової конструкції. Залежно від того, розглядаються засновки у кількісному або якісному (об’ємному чи змістовному) сенсі, розрізняют два її формулювання:
1) Dictum de omni et de nullo (сказане про усе і ні про одне): усе, що стверджується або заперечується про клас предметів у цілому, стверджується або заперечується і про частину або окремий елемент цього класу;
2) Nota notae est nota rei (ознака ознаки речі є ознакою самої речі).
Аксіома силогізму є вихідною логічною основою, на якій ґрунтується вся силогістика.
Серед умовиводів із складних суджень є традиційні види, які зазвичай класифікують і називають за типом суджень-засновків: суто умовні (усі засновки – умовні судження); умовно-категоричні, де один засновок – умовне судження, другий – просте категоричне; розділово-категоричні (засновки – розділове і категоричне судження) та умовно-розділові (лематичні) з декількома умовними і одним розділовим засновком. Визначення їх правильності ґрунтується на знанні правильних модусів (різновидів) цих умовиводів і співставленні логічної форми висновку, який перевіряється, з формою правильних модусів.
Модуси прямих дедуктивних умовиводів
| Суто умовні | Умовно-категоричні | Розділово-категоричні Modus tollendo ponens | Розділово-категоричні Modus ponendo tollens | Умовно-розділові | |
| A→B,B→C A→C | Modus ponens A→B, A B | AVB, ~A B |  A A  B, A
~B B, A
~B
| A→C B→C AVB C | Проста конструктивна дилема |
| A→B,B→C ~C→ ~A | Modus tollens A→B, ~B ~A | AVB, ~B A |  A A  B, B
~А B, B
~А
| A→C B→D AVB CVD | Складна конструктивна дилема |
| A→B B→C… Y→Z A→Z | Неправильний модус A→B, ~A ~B |  A A  B, ~A
B B, ~A
B
| Неправильний модус AVB, A ~B | A→B A→C ~BV~C ~A | Проста деструктивна дилема |
| С. умовний силогізм вживається рідко | Неправильний модус A→B, B A |  A A  B, ~B
A B, ~B
A
| Неправильний модус AVB, B ~A | A→B C→D ~BV~D ~AV~C | Складна деструктивна дилема |
Для перевірки правильності умовиводів із складних суджень, що не зводяться до перерахованих типів, використовується передусім табличний метод, заснований на тому, що між засновками і висновком дедуктивного умовиводу повинно існувати відношення логічного слідування, яке означає, що висновок не може бути хибним, якщо усі засновки істинні.
Розглянемо приклад: «Усі студенти, які навчаються на цьому факультеті, здібні або старанні. Якщо вони старанні, то регулярно займаються. Отже, якщо студенти цього факультету не займаються регулярно, то вони здібні». Перевіримо, чи правильний цей умовивід. Запишемо його форму:
(p v q), (q → r) => (~r → p), де p означає «студент цього факультету здібний», q – «студент цього факультету старанний», r – «студент регулярно займається», => означає «слідує». Побудуємо загальну таблицю для усіх суджень, що входять до складу умовиводу, відокремивши висновок від засновків двома вертикальними рисками:
| № | p | q | r | (p v q) | (q → r) | (~r → p) | |
| і | і | і | і | і | і | ||
| і | і | х | і | х | і | ||
| і | х | і | і | і | і | ||
| і | х | х | і | і | і | ||
| х | і | і | і | і | і | ||
| х | і | х | і | х | х | ||
| х | х | і | х | і | і | ||
| х | х | х | х | і | х |
У цій таблиці нас цікавлять рядки, де засновки разом істинні. Це рядки 1, 3, 4, 5. Дивимось, чи не виходить помилковим висновок хоч б в одному із зазначених рядків. Як бачимо, висновок скрізь у цих рядках є істинним. Отже, висновок правильний.
Правильність умовиводу не завжди зручно перевіряти за таблицею, оскільки вже при чотирьох змінних таблиця містить 16 рядків, а при п’яти змінних – 32 рядки, тому частіше використовується скорочений спосіб перевірки. Він полягає у міркуванні «від протилежного», тобто від припущення, що висновок є неправильним. Починаємо міркувати: якщо умовивід неправильний, то висновок може бути помилковим за наявності усіх істинних засновків. У нашому випадку:
(p v q), (q → r), (~r → p)
і і х
Далі істиннісні значення, отримані з цього припущення, переходять на дрібніші частини формул аж до пропозиційних змінних. Яким чином це робиться, продемонструємо на нашому прикладі: (p v q), за припущенням, є істинним, але нічого не можна сказати про значення р і q, крім того, що хоча б одне з них є істинним (за табличним визначенням диз’юнкції). Також не можна отримати певні значення q і r з істинності формули (q → r). Зате з помилковості (~r → p) виходить, що ~r – і, р – х (імплікація хибна лише у тому випадку, коли у ній істинний антецедент і хибний консеквент). З істинності ~r випливає хибність p. Потім винайдені значення p та r підставляємо в усі структурні одиниці з цими літерами, оскільки р скрізь означає одне судження та r скрізь означає одне судження. Таким чином, виходить:
(p v q), (q → r), (~r → p)
х і і х і х х х
Тепер з істинності (p v q) при тому, що р – х, отримуємо істинність q (у істинній диз’юнкції має бути хоча б одна істинна складова). Підставляємо це значення q у другий засновок і приходимо до протиріччя: якщо антецедент формули (q → r) істинний, а консеквент хибний, то імплікація має бути хибною, а за нашим припущенням, вона істинна.
(p v q), (q → r), (~r → p)
х і і і і х і х х х
Якщо наше припущення призвело до протиріччя, то воно помилкове, а істинним є зворотне – не може бути помилковим висновок за наявності істинних засновків, а це означає, що умовивід є правильним.
Якщо ж протиріччя з подібного припущення не виникає, то воно не спростовується, і загальний висновок буде таким, що логічного слідування немає, тобто умовивід невірний. Якщо ми отримаємо декілька варіантів значень, то висновок про правильність умовиводу можна зробити лише тоді, якщо усі вони призводять до протиріччя, і навпаки, якщо буде знайдений варіант істиннісних значень, який не призводить до протиріччя, то умовивід неправильний.
Словник – мінімум
Умовивід – форма мислення, за допомогою якої з одних думок (засновків) одержують нові думки – висновки.
Безпосередній умовивід – умовивід, доскладу якого входить лише один засновок (і звичайно ж, - висновок).
Перетворення – перебудова судження, внаслідок якої з вихідного утворюють нове рівнозначне судження, але протилежної якості: стверджувальне судження перетворюється на заперечне, а заперечне - на стверджувальне.
Обернення – перебудова судження, внаслідок якої суб’єкт і предикат міняються місцями. При цьому якість судження зберігається, а кількість може змінюватися.
Протиставлення – перебудова судження, в ході якої одночасно здійснюються і перетворення, і обернення в тій чи іншій послідовності.
Простий категоричний силогізм – опосередкований дедуктивний умовивід, який складається з двох засновків (посилань) і висновку, які є категоричними судженнями.
Ентимема – скорочений силогізм, у якому одне з трьох суджень, що входять до його складу не висловлюється , хоч і мається на увазі .
Розділовий умовивід – опосередкований дедуктивний умовивід, до складу якого входять розділові судження, а перший засновок завжди є розділовим.
Розділово – умовний умовивід – розділовий умовивід, в якому один із засновків (перший) є розділовим судженням, а інші засновки (їх кількість дорівнює кількості членів розділового судження – засновку, тобто кількості диз’юнктів) – умовні судження.
Умовний умовивід – опосередкований дедуктивний умовивід, до складу якого входять умовні судження; перший засновок у ньому завжди є умовним.
Суто умовний умовивід – умовний умовивід, в якому обидва засновки і висновок є умовними судженнями.
Умовно – категоричний умовивід – умовний умовивід, в якому другий засновок і висновок є категоричними судженнями.
Умовно – розділовий (лематичний) умовивід – умовний умовивід, до складу якого входять крім умовних ще й розділові (одне чи два) судження.
Контрольні питання
1. Чим умовиводи відрізняються від інших форм мислення?
2. Чим відрізняються безпосередні умовиводи від опосередкованих?
3. Які умовиводи називаються безпосередніми?
4. Що називається перетворенням судження?
5. Які труднощі виникають при перетворенні суджень?
6. Що таке обернення?
7. Які труднощі виникають при оберненні?
8. Від чого залежить кількість судження – висновку при оберненні?
9. Що називається протиставленням?
10. Яка специфіка протиставлення предикатові?
11. Що таке протиставлення суб’єктові?
12. Що характерне для дедуктивних умовиводів?
13. На які види поділяються дедуктивні умовиводи залежно від того, з яких суджень вони складаються?
14. Які визначення простого категоричного силогізму ви знаєте і в чому полягає перевага кожного з них?
15. Як встановити структуру силогізму?
16. Як встановити, який із засновків є більшим, а який – меншим?
17. Як встановити середній термін силогізму?
18. Які ви знаєте правила термінів силогізму?
19. Які ви знаєте правила засновків?
20. Чим відрізняються фігури силогізму?
21. Які ви знаєте правила фігур?
22. Чому люди часто вдаються до ентимем?
23. Які види ентимем ви знаєте?
24. Який силогізм називається складним?
25. Які ви знаєте модуси розділово – категоричного умовиводу?
26. Які модуси має розділово – умовний умовивід?
27. Яка будова умовно – категоричного умовиводу?
28. Які ви знаєте модуси умовно – категоричного умовиводу?
Завдання для контролю та тренування
1. Визначте, чи правильні ці силогізми. Обґрунтуйте свою думку теоретично (з допомогою правил термінів силогізму), а також графічно (з допомогою кругових схем):
а) Всі прості числа діляться лише на одиницю і самі на себе.
Число 13 ділиться лише на одиницю і саме на себе.
Отже, число 13 просте число.
Б) Всі прості числа діляться лише на одиницю і самі на себе.
Це число не є простим.............................................................
Це число не належить до тих чисел, які діляться лише на одиницю і самі на себе.
В) Всі, хто називає нас людьми, говорить істину.
Всі хто називає нас аморальними, називає нас людьми.
Отже, всі, хто називає нас аморальними, говорить істину.
2. Які правила фігур порушено в таких силогізмах:
а) Всі протони є елементарними частками.
Нейтрони – елементарні частки..........................................................
Отже, нейтрони є протонами.
Б) Зірки – небесні тіла.
Всі зірки мають кулясту форму...........................................................
Отже, принаймні деякі з тих (тіл), що мають кулясту форму, - небесні тіла.
3. Визначте модуси силогізмів, перелічених у завданні 1, 2.
Література
1. Жоль К.К. Логика в лицах и символах: [Частина книги: Глава 2. В гостях у Шерлока Холмса]. – М.: Восток-Запад, АСТ, 2006. – С. 67-118.
2. Ішмуратов А.Т. Вступ до філософської логіки: Підручник для студентів та аспірантів гуманітарних спеціальностей вищих навчальних закладів: [Частина книги: Розділ 16. Силогістика і сучасна логіка. 16.3. Дедуктивний принцип силогістики]. – К.: Абрис, 2007. – С. 223-224.
3. Коэн М., Нагель Э. Введение в логику и научный метод: [Частина книги: Книга І. Формальная логика. Глава V. Условные, разделительные и строго разделительные силлогизмы] / Пер. с англ. П.С. Куслия. – Челябинск, Пермь: Социум, 2010. – С. 150-167.
4. Солодухин О.А. Логика: Для студентов вуза: [Частина книги: Глава 4. Рассуждение. 4.2. Дедуктивная система натурального вывода]. – Ростов-н/Д: Феникс, 2004. – С. 109-114. – (Бібліотека ЗНУ).
Семінарське заняття № 6. Індуктивні умовиводи
План
1. Поняття про індукцію.
2. Спостереження та експеримент.
3. Повна індукція. Неповна індукція.
4. Індукція через простий перелік. Індукція через відбір фактів, які виключають випадкові узагальнення.
5. Наукова індукція. Методи встановлення причинних зв язків між явищами.
6. Зв язок індукції і дедукції.
Дата добавления: 2015-01-01; просмотров: 419; Мы поможем в написании вашей работы!; Нарушение авторских прав |