
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Первообразная. Неопределенный интеграл
Основная задача дифференциального исчисления состоит в нахождении дифференциала данной функции или её производной. Интегральное исчисление решает обратную задачу: для данной функции найти такую
найти такую  функцию F(x), производная которой равна f (x).
функцию F(x), производная которой равна f (x).
Например, для функции f (x) = x4 этому условию удовлетворяет функция
F(x) = 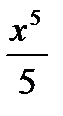 , так как F’ (x) =
, так как F’ (x) = 
Функция F(x) называется первообразной для функции f (x) , если
 .
.
Следовательно, функции  является первообразной для функции x4.
является первообразной для функции x4.
Однако она не является единственной первообразной для x4. Ими являются функции  ,
, 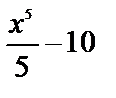 и вообще
и вообще  , где С - произвольная постоянная.
, где С - произвольная постоянная.
Оказывается, что все первообразные для любой функции f (x) даются формулой F (x) + C, где F’ (x) = f (x) и С - произвольная постоянная.
Совокупность всех первообразных для непрерывной функции называется неопределенным интеграломи обозначается

где функция f (x) - подынтегральная функция, f(x)d x - подынтегральное выражение, d x - дифференциал аргумента.
Таким образом, если F (x) какая-либо первообразная для f (x) , то

Например,

Процесс нахождения неопределенного интеграла называется интегрированиемэтой функции.
Из определения неопределенного интеграла следует, что каждой формуле дифференциального исчисления  соответствует формула
соответствует формула  в интегральном исчислении.
в интегральном исчислении.
Таблица основных интегралов
Следующие формулы интегрального исчисления получены из таблицы основных производных с добавлением к ним наиболее часто встречающихся интегралов. Заметим, что правильность всех этих формул проверяется путём вычисления производных от их правых частей.
1.  2.
2. 
3.  4.
4. 

5. 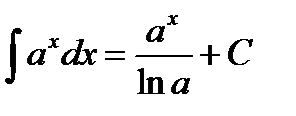 6.
6. 
7.  8.
8. 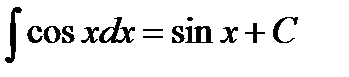
9.  10.
10. 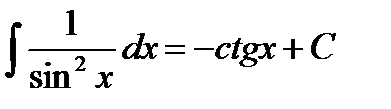
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 
|
Интегралы из этой таблицы в дальнейшем будем называть табличными интегралами.
Дата добавления: 2015-01-05; просмотров: 271; Мы поможем в написании вашей работы!; Нарушение авторских прав |