
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 3. Найти интервалы выпуклости и вогнутости и точки перегиба кривой у=х+36х2–2х3–х4.
Найти интервалы выпуклости и вогнутости и точки перегиба кривой у=х+36х2–2х3–х4.
Областью определения данной функции является множество всех действительных чисел, т. е. хЄ(–∞, +∞).
Найдем вторую производную.
у¢=1+72х–6х2–4х3.
у¢¢=72–12х–12х2= –12(х2+х–6).
Из уравнения у¢¢=0 получим абсциссу точки перегиба:
–12(х2+х–6)=0 х1= –3; х2=2.
Определим знак у¢¢ на интервалах
(–∞; –3), (–3; 2), (2, +∞).
| х | (–∞, –3) | -3 | (–3; 2) | (2; +∞) | |
| у¢¢ | – | + | – | ||
| форма кривой | выпукла 
| перегиб | вогнута

| перегиб | выпукла 
|
Найдем ординаты точек перегиба:
у(–3)=726; М1(–3; 726) – точка перегиба
у(2)=114; М2(2; 114) – точка перегиба.
На интервале (–3; 2) кривая вогнута. На интервалах (–∞; –3) и (2; +∞) – выпукла.
Вопросы для самоконтроля
1. Что называют модулем вещественного числа? Может ли модуль числа принимать отрицательные значения? Может ли модуль числа превзойти само число или равняться самому числу?
2. Что называется окрестностью точки? Как изображается окрестность на оси?
3. Какие величины называются постоянными, какие переменными? Примеры их.
4. Дайте определение функции, области ее определения и множества значений.
5. Какие способы задания функции Вам известны? Каковы преимущества и недостатки каждого способа?
6. Что называют графиком функции?
7. Какая функция называется возрастающей (убывающей) на отрезке? Особенности графика монотонной на отрезке функции.
8. Какая функция называется периодической? Особенности ее графика.
9. Какая функция называется четной (нечетной)? Особенности графика четной (нечетной) функции. Какими будут: 1) произведение четной и нечетной функций; 2) произведение двух четных или произведение двух нечетных функций?
10. Какова область определения: 1) многочлена; 2) линейной функции; 3) квадратного трехчлена; 4) показательной функции; 5) логарифмической функции?
11. Когда число А называется пределом функции ƒ(х) при х®х0?
12. Что называется левосторонним (правосторонним) пределом функции в точке? Какова связь между пределом и односторонними пределами?
13. Какая функция называется бесконечно малой при х®х0?
14. Если функции α(х) и β(х) – бесконечно малые при х®х0, что можно сказать о функциях при х®х0: α(х)·β(х); α(х)±β(х); 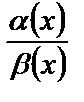 ;
;  ?
?
15. Укажите, при каком значении х0 будет бесконечно малой при х®х0 функция: 1) sin x; 2) cos x; 3) lg x.
16. Какая функция называется непрерывной в точке? Как исследовать функцию на непрерывность в данной точке?
17. Какие выражения называются неопределенными? Что значит раскрыть неопределенность? Каковы правила раскрытия неопределенностей  ?
?
18. Когда х0 называют точкой разрыва? Дайте определение точки разрыва первого рода (второго рода).
19. Что называется производной функции в точке?
20. У какой функции производная постоянна (не зависит от точки, в которой она вычисляется)?
21. Как ведет себя функция на промежутке, где ее производная только положительна (отрицательна)?
22. Дать определение касательной к кривой? Каково ее уравнение?
23. Каков физический смысл производной?
24. Записать сложную функцию у=ƒ(х), если: 1)  ,
,  ,
,  ,
,  , 2)
, 2)  ,
,  .
.
25. Записать в виде цепочки простейших функций сложную функцию:
1)  , 2)
, 2)  .
.
26. Как найти производную сложной функции?
27. Дайте определение максимума (минимума) функции в точке. Что можно сказать о знаке приращения функции в достаточно малой окрестности точки максимума (минимума)?
28. Каковы необходимые условия существования экстремума функции? Каков их геометрический смысл?
29. Каково правило нахождения наибольшего и наименьшего значений функции на отрезке?
30. Дайте определение выпуклости (вогнутости) кривой на промежутке.
31. Каково правило отыскания интервалов выпуклости и вогнутости кривой?
32. Точка перегиба кривой. Как ее найти?
33. Правило Лопиталя, когда и как его применяют?
Дата добавления: 2015-01-05; просмотров: 368; Мы поможем в написании вашей работы!; Нарушение авторских прав |