
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача № 6.
Исследовать функцию  и построить ее график.
и построить ее график.
1. Данная функция является многочленом (можно раскрыть скобки, получим многочлен третьей степени), поэтому она определена, непрерывна и дифференцируема при любых х.
2. Найдем производную.
 .
.
Из уравнения у¢=0 найдем критические точки: 3х·(х–2)=0, х1=0, х2=2.
Исследуем их.
| х | (–∞, 0) | (0; 2) | (2; +∞) | ||
| у¢ | + | – | + | ||
| у | |||||
| возрастает | max | убывает | min | возрастает |
3. Итак, функция возрастает на интервалах (–∞, 0) и (2, +∞), убывает на интервале (0; 2), имеет максимум при х=0 и минимум при х=2:
уmax=у(0)=4; уmin=у(2)=0.
4. Найдем вторую производную.
у¢¢=6·(х-1).
Кривая выпукла там, где у¢¢ < 0, т. е. 6·(х–1) < 0, х < 1.
Кривая вогнута там, где у¢¢ > 0, т. е. х > 1.
Итак, на интервале (–∞, 1) кривая выпукла; а на интервале (1, +∞) – вогнута.
5. Точку перегиба найдем из уравнения у¢¢=0. Таким образом, х=1 – абсцисса точки перегиба, т.к. эта точка разделяет интервалы выпуклости и вогнутости кривой. Ордината точки перегиба: у(1)=2.
График функции у=(х+1)·(х–2)2 пересекает ось Ох при у=0, т. е. при х= –1 и х=2;
пересекает ось Оу при х=0, т. е. при у=4. Мы получили три точки: (–1; 0), (2; 0), (0; 4).
Все полученные точки внесем в таблицу, добавив соседние с ними.
| х | –2 | –1 | 
| 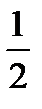
| 
| 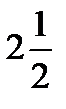
| ||||
| у | –16 | 3 
| 
| 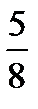
| 
| |||||
| max | перегиб | min |

Рис. 28 Кривая у=(х+1)(х–2)2.
Дата добавления: 2015-01-05; просмотров: 238; Мы поможем в написании вашей работы!; Нарушение авторских прав |