Правила вычисления производных

Производная сложной функции.

Если у=ƒ(и), и=φ(х), то у¢(х)=ƒ¢(и)·φ¢ (х).

Производная суммы.

Если у(х)=и(х)+v (х), то у¢ (х)=и¢ (х)+v¢ (х)

Производная произведения.

Если у(х)=и(х)·v(х), то у¢=и¢·v+u·v¢.

В частности, (с·и)¢=с·и¢, т. е. постоянный множитель выносится из-под знака производной. Легко убедиться, что

(u²)¢=2u·u¢, (u³)¢=3u²·u¢, … , (uⁿ)¢=n·u^n–1·u¢.

Производная частного.

Если , то .

Приведем и таблицу производных.

Таблица производных

1. (с)¢=0	Для сложной функции: если и=и(х), то:
2. (х)¢=1
3. (хα)¢=α·хα–1, а – любое действительное число. 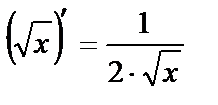.	3.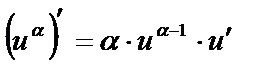
4. (ах)¢=ах·ln а	4.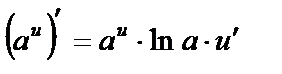
5. (logax)¢= .	5.
6. (sin x)¢=cos x	6.
7. (cos x)¢= –sin x	7.
8. (tg x)¢=	8.
9. (ctg x)¢=	9.
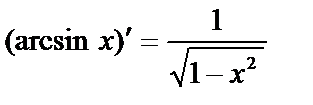
10.	10.
11.	11.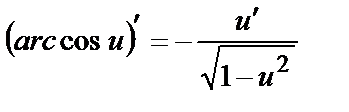
12.	12.
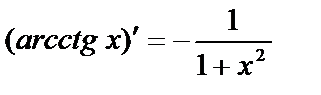
13.	13.

При дифференцировании следующих функций укажем формулы и правила, которыми будем пользоваться.

Найти производные следующих функций.