
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Бесконечно малые и бесконечно большие функции
Определение. Бесконечно малой при х®х0 называется функция α(х), предел
которой при х®х0 равен нулю, т. е.

Для бесконечно малых верны теоремы о пределах функций, а именно:
–сумма конечного числа бесконечно малых функций есть функция бесконечно малая;
–произведение бесконечно малых есть функция бесконечно малая;
–произведение бесконечно малой на постоянную есть функция бесконечно малая;
–произведение бесконечно малой на функцию ограниченную есть функция бесконечно малая.
Например, α1(х)=(х–2)2 – функция бесконечно малая при х®2.
α2(х)=sin x – функция бесконечно малая при х®π.
α3(х)=х2–3х+2 – функция бесконечно малая при х®1.
Обратимся теперь к рассмотрению функций, значения которых в окрестности точки х0 не ограничены.
Определение.Функция ƒ(х) называется бесконечно большой
при  , если для любого положительного числа М
, если для любого положительного числа М
найдется такое положительное число δ, что для каждого х
из δ-окрестности точки х0 выполняется неравенство
|ƒ(х)| > М.
Примером такой функции является функция tg х при  .
.
Функция  при х®0 также является бесконечно большой. Если ƒ(х) – бесконечно большая при х®х0 функция, то записывают:
при х®0 также является бесконечно большой. Если ƒ(х) – бесконечно большая при х®х0 функция, то записывают:
 .
.
Здесь знак ∞ (бесконечность) указывает, что функция не имеет предела и является бесконечно большой.
Сформулируем теорему о связи бесконечно малой и бесконечно большой функций.
Теорема. Если функция α(х) – бесконечно малая при х®х0, то  –
–
бесконечно большая функция при х®х0.
Если ƒ(х) – бесконечно большая функция при х®х0, то
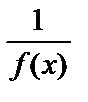 – бесконечно малая функция при х®х0.
– бесконечно малая функция при х®х0.
Например, если sin x – бесконечно малая при х®0, то 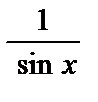 – бесконечно большая при
– бесконечно большая при  . Или при х®3 функция х–3®0, а функция
. Или при х®3 функция х–3®0, а функция 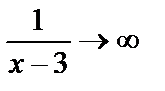 .
.
Заметим, что отношение любой функции, стремящейся к конечному пределу, и функции бесконечно малой является функцией бесконечно большой.
Поэтому,  , т. к.
, т. к.  , а
, а 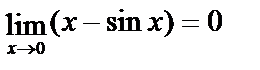 .
.
Рассмотрим поведение функций при неограниченном возрастании аргумента х. Говорят х®∞ (неограниченно возрастает по абсолютной величине), если для любого числа М > 0 переменная х примет значение
|х| > М
Можно говорить о пределе функции при х®∞. Если при этом существует предел А функции ƒ(х), то записывают

Все рассмотренные теоремы и правила вычисления предела справедливы и в этом случае.
Например,  – бесконечно малая функция при х®∞, т. к.
– бесконечно малая функция при х®∞, т. к. 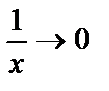 .
.
Дата добавления: 2015-01-05; просмотров: 312; Мы поможем в написании вашей работы!; Нарушение авторских прав |