
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Укажем некоторые теоремы о пределах функций.
Пусть существует  и
и  .
.
Теорема 1. Предел алгебраической суммы двух функций равен такой же
сумме пределов слагаемых, т. е.
 .
.
Теорема 2.Предел произведения функций равен произведению их пределов, т. е.

Теорема 3. Предел частного от деления двух функций равен частному от
деления их пределов, если предел делителя не равен нулю,
т. е.
 , если
, если 
Теорема 4. Пусть в некоторой окрестности точки х0 выполняются
неравенства
 и
и

Тогда существует  равный числу А, т. е.
равный числу А, т. е.

Теорема 5.Если  и
и  и в некоторой окрестности
и в некоторой окрестности
точки х0 ƒ(х) £ φ(х), то и 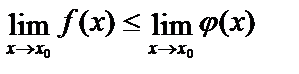 , т. е. А £ В.
, т. е. А £ В.
Применяя эти теоремы, вычисляем

Сравнивая полученное выражение с данным алгебраическим выражением, видим, что вместо переменной х всюду записан lim x, т. е.

Сформулируем правило:
Для вычисления предела алгебраического выражения следует всюду вместо переменной подставить ее предел и подсчитать результат, если при этом нигде не встретилось деление на нуль.
Рассмотрим теперь функции, стремящиеся к нулю и действия с ними.
Дата добавления: 2015-01-05; просмотров: 253; Мы поможем в написании вашей работы!; Нарушение авторских прав |